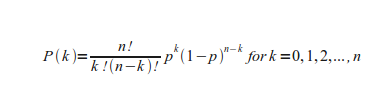Table of Contents
[1] The apparatus of a critical edition of the biblical text can be encoded as a tabular structure called a data matrix. By counting how often witnesses disagree in their readings, another tabular structure called a dissimilarity matrix is obtained which records the distance between each pair of witnesses. This article begins by applying statistical reasoning to determine what constitutes a statistically significant distance between two witnesses and how sample size affects the margin of error for a distance estimate. Following this, two modes of multivariate analysis called “multidimensional scaling” and “divisive clustering” are introduced then applied to data extracted from the apparatus of the Letter to the Hebrews in the fourth edition of the United Bible Societies' Greek New Testament (UBS4).[1]
[2] The results offer fresh ways to comprehend relationships among ancient witnesses of the text. Multidimensional scaling produces a map that reveals the structure of the “textual space” occupied by these witnesses while divisive clustering produces a tree-like structure that progresses from broad to narrow categories. Some of the clusters revealed by the analysis are evocative of the conventional “Alexandrian,” “Byzantine,” and “Western” text-types. However, the analysis results also exhibit important differences relative to these text-types.
[3] It is natural to ask what each cluster revealed by the analysis represents and how the overall picture came to have its present form. A geographical interpretation can be applied to the multidimensional scaling map whereby concentrations of witnesses are correlated with regions around the Mediterranean rim. If this is a valid interpretation of the data then Streeter's theory of local texts deserves to be reconsidered.
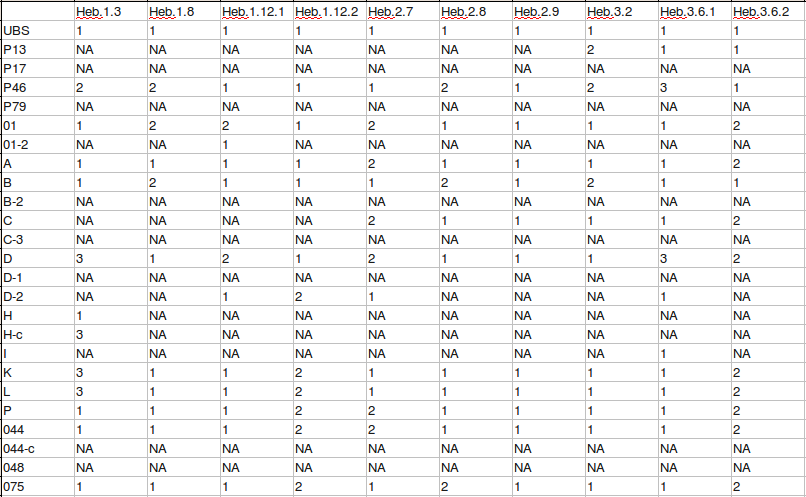
[4] The apparatus of a critical edition specifies the readings of various witnesses to the text at places where the witnesses differ. A variation unit is a place where the text varies across witnesses, and is comprised of the readings encountered at that site. In the case of the New Testament, where thousands of witnesses survive, critical editions usually report only substantive variations (i.e. those which affect the meaning), thus sparing the reader from a miriad of orthographic variations (i.e. differences of spelling, diacritics, and punctuation which don't affect meaning). Editions which take this approach include UBS4 and the 27th edition of the Nestle-Aland Novum Testamentum Graece (NA27).[2] NA27 covers many more variation units than UBS4 but, due to space restrictions, does not always include the full attestation (i.e. list of supporting witnesses) for each reading. Instead, the reader has to consult the introduction and an appendix to see whether absence of a witness from the attestation for a reading is because it is undefined at the relevant place or has been subsumed under a set of “constant witnesses.” By contrast, UBS4 reports fewer variation units but gives the full attestation for each reading of a variation unit. Thus, absence of a witness from the attestations of all readings of a variation unit in UBS4 implies that the witness is undefined there, perhaps because it is illegible or is a version whose back-translation into Greek cannot be taken as support for a single reading. This makes the UBS4 apparatus a more convenient basis for producing a data matrix.
[5] A data matrix is a grid which shows the reading of each witness at each variation
unit. By convention, rows are devoted to witnesses and columns to variation units. At the
intersection of each row and column is a cell which specifies the reading of the witness at
that variation unit. Instead of placing the entire reading in the cell, it is enough to encode
the reading as a numeral using a one-to-one correspondence between readings and numerals for
each variation unit. While the assignment of numerals to readings is arbitrary, I prefer to
give the first reading of a variation unit in the UBS4 apparatus the numeral 1,
the second 2, the third 3, and so on. A special code,
NA, which stands for “not available,” is used when the reading of
a witness cannot be confidently determined for the variation unit in question.
[6] Taking the UBS4 apparatus of Hebrews as an example, a variation unit with three readings is found at Heb 1:3:[3]
τῆς δυνάμεως αὐτοῦ, καθαρισμόν (01 A B H* P 044 075 0150 33 81 436 1175 1962 2464 itt, v vg syrpal arm geo1 Didymusdub Cyril John-Damascusmss)
τῆς δυνάμεως, δι᾽ ἑαυτοῦ καθαρισμόν (P46 0243 6 424c 1739 1881*)
τῆς δυνάμεως αὐτοῦ, δι᾽ ἑαυτοῦ (D Hc K L 104 256 263 365 424* 459 1241 1319 1573 1852 1881c 1912 2127 2200 Byz Lect itar, b, comp, d vgms syr(p), hcopsa, bo, fay (eth) geo2 slav Chrysostom John-Damascus Augustine Varimadum)
[7] Encoding these readings as numerals produces a single column of the data matrix. Including all 44 variation units in the UBS4 apparatus of Hebrews produces a data matrix with 154 rows and 44 columns.[4] A separate row is devoted to each scribe and corrector of a manuscript. Some sigla are reformatted to facilitate the eventual plotting of analysis results. In particular, superscripts are replaced with inline forms, and Gregory-Aland numbers are employed for majuscules not represented by Roman letters. Thus, for example, P46 becomes P46, Codex Sinaiticus is represented by the Gregory-Aland number 01, Codex Vaticanus is represented by the letter B, and syrpal becomes syr-pal. This article employs these reformatted sigla from this point forwards.
[8] Analysis can begin once the data matrix is in hand. Some analytical methods operate directly on the data matrix while others begin with a dissimilarity matrix constructed by calculating the distance between each pair of witnesses.
[9] Dissimilarity is a measure of how unlike two objects are with respect to each other. When calculating the dissimilarity of two objects contained in a data matrix, it is important to compare them in a meaningful way. Data which encodes the state of an object with a numeral is called “nominal” because each numeral simply nominates the state. Even though the state is represented by a numeral, it does not make sense to compare the encoded states on any basis except equivalence. (In the present case, objects are witnesses and states are readings.) Comparisons on the basis of order, magnitude, or ratio are usually meaningless for nominal data.[5]
[10] A measure called the “simple matching distance” is suitable for quantifying the dissimilarity between two witnesses whose readings are encoded as nominal data.[6] This distance is calculated by operating on the data matrix as follows:
Extract the rows corresponding to the two witnesses being compared.
Extract the columns where both witnesses are defined (i.e. neither has
NA).Count the number of extracted columns where the readings disagree.
Divide this number of disagreements by the number of extracted columns to obtain the distance.
[11] As an example, in the rows of the Hebrews data matrix devoted to witnesses P46 and B, there are 23 columns in which the readings of both are defined. Of these, three have different readings. The simple matching distance between P46 and B based on this sample of variation units is therefore 3/23, or 0.130.[7]
[12] The significance of a distance between two witnesses is affected by certain statistical considerations. Firstly, a range of distances can be expected to occur if the readings of two witnesses are randomly selected from the available pool. Only distances outside this range are significant in a statistical sense. Secondly, the distance between a pair of witnesses calculated from a sample of variation units is only an estimate of the actual distance that would be obtained if every variation unit was counted. A statistical analysis gives a range of values that is likely to include the actual value. Finally, the relative size of the range of values increases as the sample size decreases. (In the present case, the sample size is the number of variation units.) For this reason, the utility of a distance estimate decreases as the the sample size becomes smaller.
[13] A range of numbers of disagreements can be expected to occur between two witnesses that have no genetic relationship if their readings are, in effect, random selections from the available pool. To illustrate, consider two randomly generated “witnesses” with ten variation units where each variation unit has two equally probable readings:[8]
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
[14] The distance between these two is 0.7, corresponding to seven out of ten disagreements. If the same kind of trial is performed many times then the resulting distribution of disagreements conforms to the binomial distribution:[9]
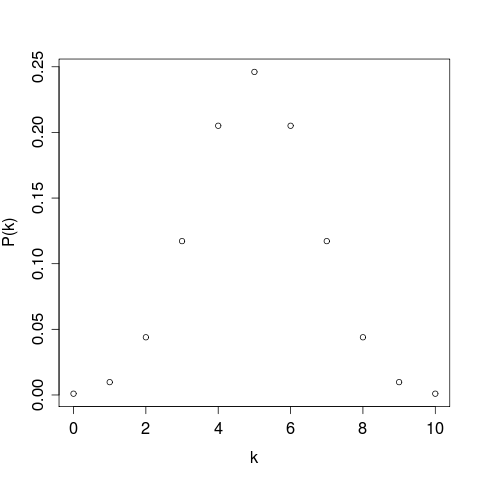
[15] Plotting this equation for ten trials and a probability of disagreement of 0.5 shows the nature of the distribution:
[16] Any number of disagreements between zero and ten out of ten is possible, but numbers near the centre of the range are more likely to occur than those in the upper (i.e. right-hand) or lower (i.e. left-hand) “tails” of the distribution.
[17] Given a knowledge of the distribution of distances, it is possible to calculate how often a particular distance is likely to occur by chance. By choosing a sufficiently small probability level, one can assert that any distances with an even smaller probability of chance occurrence are significant from a statistical point of view. This small probability is called an alpha level, and for this kind of study is often chosen to be 0.05 (i.e. 5%). Once the alpha level is selected, it is possible to calculate corresponding minimum and maximum distances called critical limits. The probability of a smaller or greater distance occurring by chance is then less than or equal to the alpha level. Thus, choosing an alpha level of 0.05 means that distances more extreme than the critical limits have less than or equal to one chance in twenty of occurring.
[18] The following table gives critical limits of distance calculated for various numbers of variation units by assuming that each one has two equally probable readings:[10]
| Number | Lower limit | Upper limit |
|---|---|---|
| 10 | 0.200 (2/10) | 0.800 (8/10) |
| 50 | 0.360 (18/50) | 0.640 (32/50) |
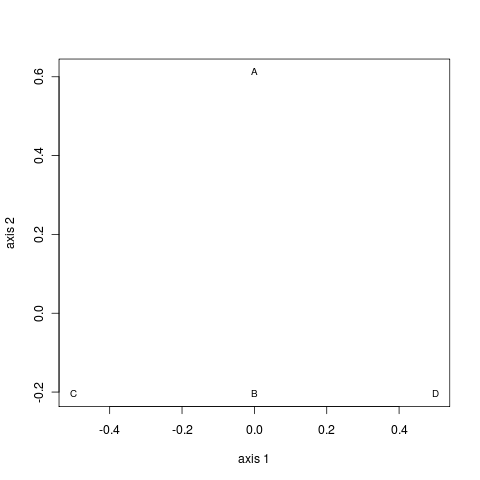
| 100 | 0.400 (40/100) | 0.600 (60/100) |
| 500 | 0.456 (228/500) | 0.544 (272/500) |
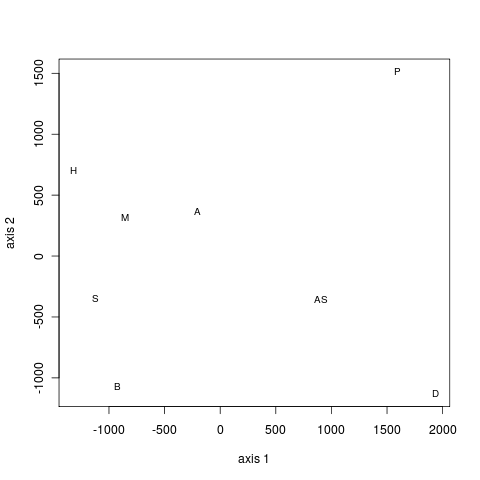
| 1000 | 0.469 (469/1000) | 0.531 (531/1000) |
[19] The relative width of the central range between lower and upper limits increases as the number of variation units decreases. This central range corresponds to distances which are not considered to be significant. If the number of variation units is five or less, the central range expands to cover all possible distances. Consequently, it is a waste of time to calculate a distance for such a small sample size. The same applies if one prefers to calculate a percentage of agreement rather than a distance.
[20] Real variation units do not conform to the special case of two equally probable readings. Instead, each variation unit may have more than two readings, and each reading has its own probability of occurrence. Estimating critical values of distance is more difficult in these circumstances but is still achievable. The first step is to estimate the probability of random disagreement for each variation unit as follows:
Estimate the probability of each reading in the variation unit by counting the number of witnesses that support the reading (ri) then dividing by the total number of witnesses (w) reported for the variation unit.[11]
Take the complement of the sum of squares of probabilities of readings to estimate the probability of random disagreement. That is, P(disagree) = 1 - Σ(ri/w)2.
[21] To elaborate, if two readings are chosen at random from within a variation unit then the chance of choosing the same reading twice is the square of its probability of being selected once. The squared probabilities are summed to take account of all possible ways in which two witnesses can have the same reading: both having the first reading, both having the second, or both having the third, and so on up to however many readings are contained in the variation unit being examined. The sum of squared probabilities is the estimated probability of agreement. The estimated probability of disagreement is then obtained by subtracting the probability of agreement from one. As a concrete example, the first variation unit in the UBS4 apparatus of Hebrews (Heb 1:3) reports the readings of 66 witnesses. Of these, 24 have the first reading, 6 the second, and 36 the third. The estimated probabilities of the readings are then 0.364 (24/66), 0.091 (6/66), and 0.545 (36/66), respectively. The estimated probability of random agreement is (24/66)2 + (6/66)2 + (36/66)2 = 0.438, giving an estimated probability of disagreement of 1 - 0.438 = 0.562.
[22] Once the probability of random disagreement is known for each variation unit, it is possible to calculate critical values of distance. To obtain the values by an exact calculation is an intensive computing exercise; performing such a calculation for the 44 variation units of Hebrews presented in the UBS4 apparatus would take a typical computer months to complete. Happily, one can instead use a “Monte Carlo” calculation to obtain the critical limits in a short time. This kind of calculation simulates a large number of trials using a program that generates pseudo-random numbers. Such a calculation that employs enough trials (say, 10,000) has a good chance of producing the same critical values as would be obtained by an exact calculation. To give an example, the estimated critical distances obtained by a Monte Carlo calculation for the set of variation units where the readings of both P46 and B are reported are 0.174 (4/23) and 0.565 (13/23), respectively.[12] The calculated distance between P46 and B (0.130) is less than the lower critical distance (0.174) so it can be regarded as statistically significant. That is, there is less than or equal to one chance in twenty that such a distance will occur if readings are randomly chosen from variation units where both P46 and B are reported.
[23] The UBS4 apparatus provides 44 variation units for Hebrews. This is certainly not a comprehensive account of all variation among extant witnesses. To identify all of the variation among these witnesses would require them all to be collated, and this would still miss variations that once occurred among witnesses now lost. Extant witnesses represent a small fraction of the total number ever produced. To add to the difficulty of estimating the number of variation units, there is no agreed upon way to delimit their boundaries.[13]
[24] Despite these problems, it is possible to get a rough idea of how many variation units would occur in Hebrews if a large number of the extant witnesses were compared. Since 1997, the Institute for New Testament Textual Research (INTF) in Münster, Germany, has been publishing installments of its Editio Critica Maior (ECM). The fascicles are so far limited to the Catholic Letters, where a total of 3061 variation units have been identified.[14] Based on respective word counts of 7591 and 4953 for the Catholic Letters and Hebrews, this figure implies that the ECM installment for Hebrews will contain about 2000 variation units. It follows that the 44 variation units given in the UBS4 apparatus of Hebrews represent a small sample of the total number. In view of this, it becomes important to know what sampling error applies for a distance calculated from a selection of variation units.
[25] If a sample is selected from a population then a sample statistic can be calculated to estimate a population parameter. In the present case, the population is all variation units of Hebrews, the sample is those variation units presented in the UBS4 apparatus, the sample statistic is the simple matching distance (i.e. proportion of disagreements) between two witnesses calculated from the sample of variation units, and the population parameter is the actual distance that would be obtained if all variation units were considered.
[26] A statistical analysis can be used to obtain an interval (i.e. range) of distances that one is confident contains the actual distance. This “confidence interval” specifies minimum and maximum distances between which the actual value is expected to lie. In order to obtain a confidence interval, a “confidence level” is selected then the boundaries of an interval are computed such that if many samples were randomly chosen, a proportion of confidence intervals equal to the confidence level would contain the actual value. A popular confidence level for the present kind of work is 95%.[15]
[27] If one had a comprehensive list of variations units for extant witnesses, the actual distance between two witnesses could be calculated by selecting the set of variation units where the readings of both witnesses are defined then calculating the proportion of disagreement for this set. For each variation unit where the readings of both witnesses are defined, it is only possible for the respective readings to agree or disagree. The set of all agreements and disagreements could therefore be represented as a set of observations, each observation signifying agreement or disagreement at the corresponding variation unit. If many random samples of a particular size were taken from this set and the number of disagreements in each sample counted then the result would be a distribution of numbers of disagreement. Provided that certain conditions are met, this “sampling distribution” is approximately the same as the binomial distribution corresponding to the given number of observations and the probability of disagreement in the selected variation units.[16]
[28] Once the sampling distribution is known, the limits of the confidence interval for the number of disagreements are found as follows:
Select a confidence level (e.g. 0.95).
Select upper and lower cumulative probabilities such that the difference between them is the confidence level (e.g. 0.025 and 0.975).
Choose two witnesses to compare.
Select the set of variation units where the readings of both witnesses are defined.
Count the number of variation units (n) and calculate the probability of disagreement (p) for the set.
Using the binomial distribution for n observations and probability of “success” p, find the corresponding upper and lower critical limits.
[29] The resulting confidence interval includes the critical limits and all distances between them. To give an example, there are three disagreements among the sample of 23 variation units in the UBS4 apparatus of Hebrews where the readings of P46 and B are both defined. Critical limits of 0 and 6 are obtained using the binomial distribution, 23 observations, a probability of “success” of 3/23, and cumulative probabilities of 0.025 and 0.975. One can therefore be 95% confident that the actual distance from P46 to B is between 0/23 (0.000) and 6/23 (0.261), inclusive.[17]
[30] There remains a question concerning whether the variation units in the UBS4 apparatus represent a random sample of the entire population of variation units. If, for some reason, the UBS editors chose the variation units in a way that favoured ones with a higher or lower probability of disagreement than applies for the entire population then there would be a bias that could render invalid a confidence interval calculated from those variation units.
[31] As the number of variation units in a sample decreases, the range of distances covered by the corresponding confidence interval increases. If there are too few variation units, the range extends to include all possible distances, making the associated distance estimate worthless. In view of this, it is desirable to calculate the minimum sample size required to obtain an acceptable relative width for the confidence interval. One possibility is to specify a maximum acceptable relative width of 50%, corresponding to a confidence interval that covers half of all the possible distances. Should a narrower relative width be desired, a larger sample size would be required.
[32] As discussed above, a confidence interval can be calculated with the binomial distribution, a sample size, a probability of disagreement estimated from the sample, and cumulative probabilities reflecting the preferred confidence level. The width of the confidence interval is a maximum when the probability of disagreement is one half.[18] Using this value for the probability of disagreement therefore provides a conservative estimate of the sample size required for a desired interval width. The following table presents a selection of sample sizes and corresponding relative widths obtained using a probability of disagreement of 0.5 and cumulative probabilities of 0.025 and 0.975:[19]
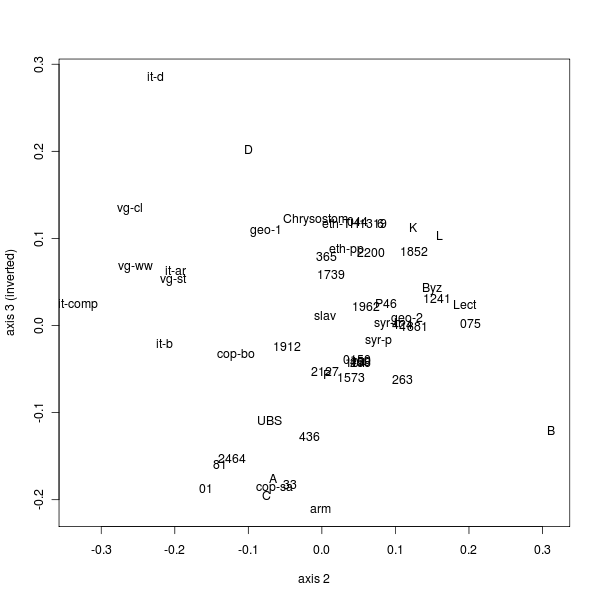
| Sample size | Lower limit | Upper limit | Relative width |
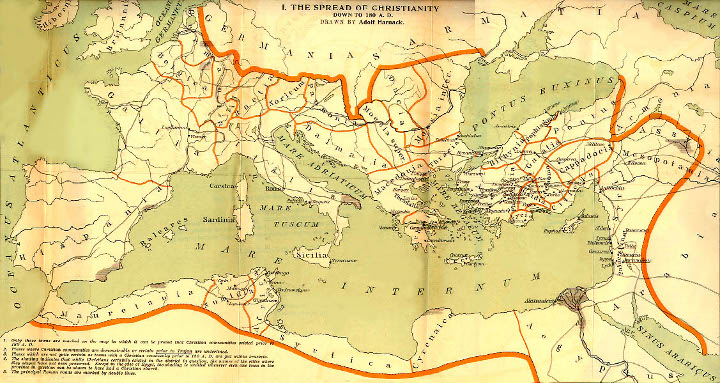
|---|---|---|---|
| 5 | 0 | 5 | 100% |
| 15 | 4 | 11 | 50% |
| 35 | 12 | 23 | 33.3% |
| 63 | 24 | 39 | 25% |
| 94 | 38 | 56 | 20% |
| 255 | 112 | 143 | 12.5% |
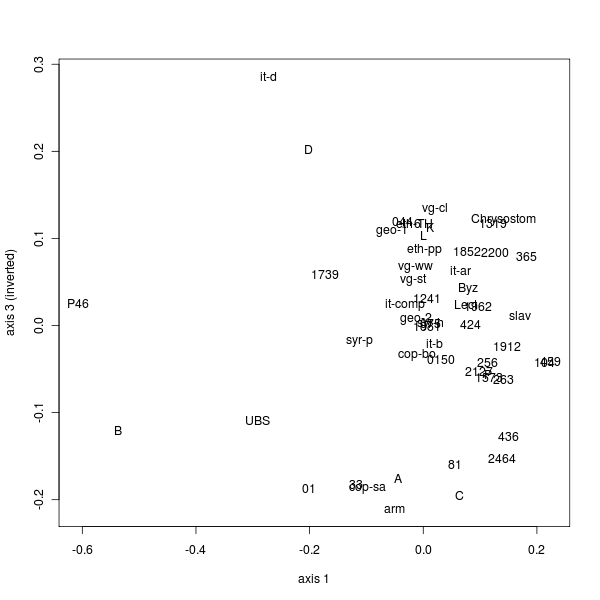
| 399 | 180 | 219 | 10% |
| 1559 | 741 | 818 | 5% |
[33] In summary, this section covers three statistical questions:
What range of distances between a pair of witnesses is likely to occur if readings are chosen at random from the available pool? If the actual distance is outside this range then it can be considered to be significant in a statistical sense.
What confidence interval applies to a distance between two witnesses estimated from a sample of variation units? One can be confident but not certain that that the actual distance is within an interval defined by critical limits calculated from a random sample of the entire population.
What is the minimum sample size required to obtain an acceptable relative width for the confidence interval calculated from a sample of variation units?
[34] A Monte Carlo calculation provides estimates for critical values which allow one to decide whether a distance between two witnesses is statistically significant. The binomial distribution is useful for calculating the confidence interval which applies to the distance between two witnesses estimated from a sample of variation units. The binomial distribution can also be used to estimate the minimum sample size required to obtain a given relative width for the confidence interval.
[35] A distance matrix is a table of distances between pairs of objects, which, in the present case, are textual witnesses. The distance matrix is square and symmetrical about its diagonal because its rows and columns relate to the same set of objects. The diagonal is comprised entirely of zeros because the distance from every object to itself is zero.
[36] The larger the sample size, the more reliable a distance estimate based on the sample. The relative width of the confidence interval associated with an estimated distance between two witnesses increases as the number of variation units in the sample decreases. A distance calculated from a sample of five or less variation units is entirely worthless because the associated confidence interval covers all possible distances. Unfortunately, increasing the sample size excludes witnesses that do not have a full complement of variation units. It is therefore necessary to reach a compromise which produces a confidence interval of tolerable width while not excluding too many interesting witnesses. For calculations related to this article, a minimum sample size of twelve has been used, corresponding to a relative interval width of just over 50% (actually 53.8%). The main reason for choosing this rather than a larger sample size is to include Codex Vaticanus (B) in the results.
[37] Three distance matrices are used to produce the results which follow:
distances between Australian cities
distances between apexes of a tetrahedron
distances between witnesses of Hebrews.
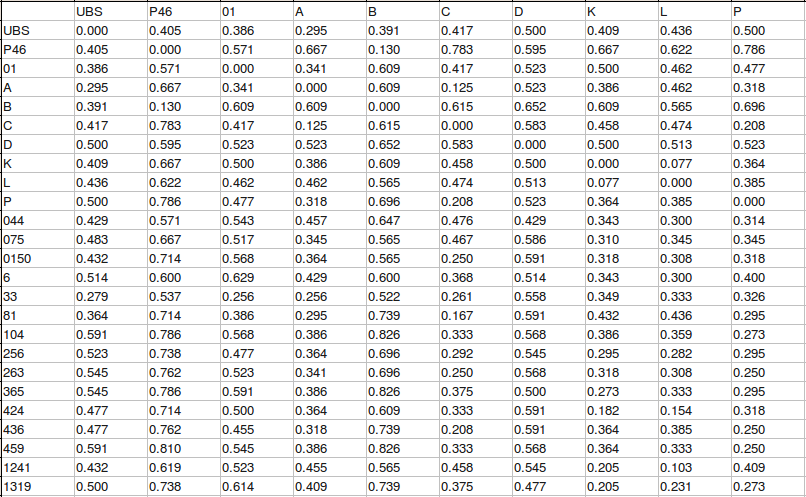
[38] The first two are contrived examples that will be used to illustrate certain aspects of multivariate analysis. The third is derived from the previously mentioned data matrix which is based on the UBS4 apparatus of Hebrews. In constructing this distance matrix, a constraint was introduced to ensure that each distance was calculated from at least twelve variation units. Due to the added constraint, only 54 objects are represented.[20]
[39] Multidimensional scaling (MDS) takes a distance matrix and derives a configuration of points in a space with a specified number of dimensions so that distances between the derived points are a best match to the original distances. As Venables and Ripley say, “We can think of 'squeezing' a high-dimensional point cloud into a small number of dimensions ... whilst preserving as well as possible the inter-point distances.”[21] The configuration found by a popular variety of multidimensional scaling called “classical” MDS minimises the sum of squared differences between the original and derived distances. In general, the maximum number of dimensions required to perfectly reproduce the original distances is one less than the number of objects. However, a reasonably good approximation can sometimes be obtained with only a few dimensions.
[40] The following cases illustrate how the given number of dimensions affects the procedure's ability to arrive at a configuration of points that adequately reflects the supplied distances. Using classical MDS to analyse the distance matrix for Australian cities with only two dimensions produces this result:
[41] The resulting map has an unconventional orientation, which is to be expected because the underlying mathematical analysis does not include any constraints concerning what should be regarded as up, down, left, or right. Consequently, it is quite appropriate to rotate or reflect such a map in order to place it in a preferred orientation. Even though it has an unconventional orientation, this map accurately reflects the relative positions of the cities included in the distance matrix. A figure called the “proportion of variance” indicates how well the procedure has managed to fit the extracted configuration of points into the available number of dimensions. In this case, the proportion of variance is 1.00 which indicates that two dimensions are sufficient to achieve a perfect fit between the original distances and those derived from the extracted coordinates. This is because the original distance matrix was derived from a flat (i.e. two-dimensional) map.
[42] Subjecting the distance matrix for the apexes of a tetrahedron to classical MDS while allowing only two dimensions produces a proportion of variance figure of 0.67, indicating that the resulting map conveys two-thirds of the analysed distance information. Allowing three dimensions produces a perfect score of 1.00. Three dimensions is sufficient to produce a perfect configuration for any four points. Two dimensions would be sufficient if all of the points were in a plane, and only one dimension would be required if they were all in a line.
[43] The distance matrix derived from the UBS4 apparatus data for Hebrews can be analysed by classical MDS as well. This matrix includes 54 objects, meaning that up to 53 dimensions would be required to perfectly convey the distance information. However, as it is hard for the human mind to cope with more than three spatial dimensions at once, it is necessary to settle for a three-dimensional representation:
[44] The proportion of variance figure for this analysis is 0.42, meaning that three dimensions explain 42% of the distance information contained in the matrix. This map is optimal in the sense that it is the best representation of the distance information that can be achieved with only three dimensions.
[45] Chatfield and Collins describe cluster analysis as follows:
The basic aim of cluster analysis is to find the “natural groupings,” if any, of a set of individuals (or objects, or points, or units, or whatever)... More formally, cluster analysis aims to allocate a set of individuals to a set of mutually exclusive, exhaustive, groups such that individuals within a group are similar to one another while individuals in different groups are dissimilar. This set of groups is usually called a partition.[22]
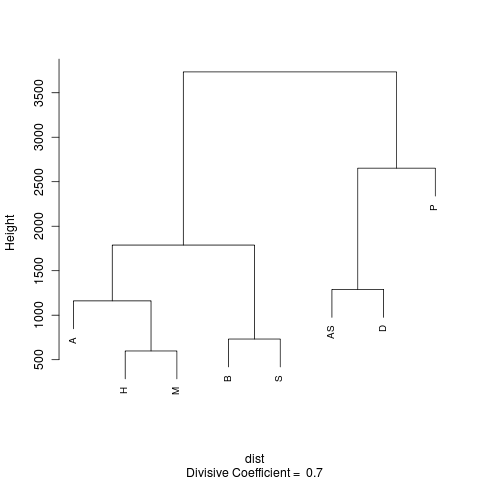
[46] This mode of analysis needs to be used with discretion. Even if the data set does not have a natural group structure, clustering techniques will still divide its members into groups. As Chatfield and Collins say, “The ability of clustering methods to detect non-existent clusters is well established.”[23] There are numerous clustering techniques, each liable to produce its own set of clusters when applied to the same data. Subjecting the distance matrix for Australian cities to a mode called “divisive clustering” produces the following result:[24]
[47] According to this chart, called a “dendrogram,” Australian cities can be partitioned in a number of ways. In order to define a partition, the tree is “chopped” at some vertical level to produce a series of clusters. For example, cutting across at a height of about 3500 km produces two clusters: one comprised of Adelaide, Hobart, Melbourne, Brisbane, and Sydney; the other containing Alice Springs, Darwin, and Perth. Other numbers of clusters can be produced by chopping the tree at other heights.
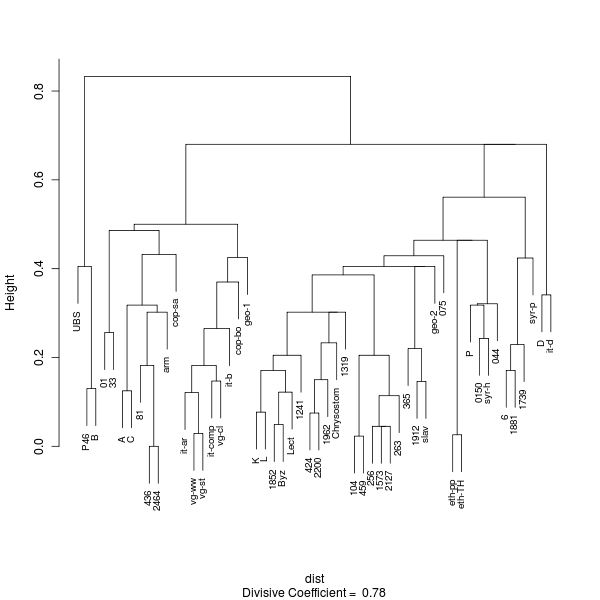
[48] Applying divisive clustering to the distance matrix for Hebrews produces this dendrogram:[25]
[49] An attempt will now be made to describe the broad outlines of what might be called the “textual space” occupied by the witnesses of Hebrews. Being based on so few variation units, sampling errors are relatively large. All observations made from these analysis results are therefore provisional.
[50] The MDS map reveals a structure in which some regions have a higher density of witnesses than others. There is a general correspondence between these regions of higher density and clusters found in the dendrogram but it is hard to say how many clusters there are. Indeed, this dendrogram is similar to one concerning which Chatfield and Collins say, “there appears to be no natural partition.”[26] It seems, therefore, that there is no clear number of clusters for the Hebrews data.
[51] To make an arbitrary choice, the dendrogram can be chopped at a height of just under 0.5 to produce six clusters:
UBS (i.e. the eclectic text preferred by the UBS editors), P46, B
01 (Sinaiticus), A, C, 33, 81, 436, 2464, cop-sa (Sahidic Coptic), arm (Armenian)
it-ar, it-b, it-comp (i.e. Old Latins); vg-cl, vg-st, vg-ww (i.e. editions of the Vulgate); cop-bo (Bohairic Coptic), geo-1 (First Georgian)
K, L, P, 044, 075, 0150, 104, 256, 263, 365, 424, 459, 1241, 1319, 1573, 1852, 1912, 1962, 2127, 2200, Byz (Byzantine majority), Lect (majority of lectionaries), syr-h (Harclean Syriac), eth-pp, eth-TH (i.e. editions of the Ethiopic), geo-2 (Second Georgian), slav (Slavonic), Chrysostom
6, 1739, 1881, syr-p (Peshitta Syriac)
D, it-d.
[52] A number of these clusters are evocative of conventional “text-types” often used to describe New Testament witnesses, namely “primary Alexandrian” (P46, B), “secondary Alexandrian” (e.g. A, C, 33, 81), “Western” (e.g. Old Latins it-ar, it-b, it-comp), and “Byzantine” (K, L, ..., Chrysostom).[27] At the same time, the dendrogram has a number of unexpected features: the cluster associated with “primary Alexandrian” witnesses is quite distant from the others; the “secondary Alexandrian” is more closely affiliated to the “Western” than the “primary Alexandrian” cluster; Codex Sinaiticus (01) and the Armenian (arm) fall into the “secondary Alexandrian” cluster; the Sahidic and Bohairic versions of the Coptic occupy different clusters; and the cluster comprised of D and it-d, which are the Greek and Latin sides of Codex Claromontanus, stands apart from the “Western” cluster. Some of these surprises may be attributable to sampling error; a larger sample would have to be analysed in order to confirm them.
[53] An association between the three minuscules of the fifth cluster (i.e. 6, 1739, 1881) has already been noticed by Waltz.[28] Surprisingly, the dendrogram indicates that this cluster is more closely related to the fourth, which contains “Byzantine” witnesses such as K and L, than to the first, second, or third, which might be described as “Alexandrian” or “Western.” It is also surprising to see that the Peshitta Syriac is located here.
[54] Other numbers of clusters are produced by cutting the dendrogram at different heights. If, say, the division was made at a height of 0.6 then there would be only four: the second and third clusters of the six-way partition would be combined into a larger entity, as would the fourth and fifth. Chopping the dendrogram at a height 0.45 produces nine clusters: the second of the six-way partition splitting into two and the fourth splitting into three. Hopefully, these examples are enough to demonstrate the arbitrary nature of any choice concerning the number of clusters.
[55] Overall, the dendrogram paints a picture of diffuse clusters which have points of contact with the conventional text-types yet differ in significant ways. The usefulness of dividing the tradition into “Alexandrian,” “Byzantine,” “Western,” and, perhaps, “Caesarean” text-types has long been questioned. In 1965, Kurt Aland, then director of the INTF, wrote:
It is impossible to fit the papyri, from the time prior to the fourth century, into these text-types, to say nothing of trying to fit them into other types, as frequently happens. The simple fact that all these papyri, with their various distinctive characteristics, did exist side by side, in the same ecclesiastical province, that is, Egypt, where they were found, is the best argument against the existence of any text-types, including the Alexandrian and the Antiochian. We still live in the world of Westcott and Hort with our conception of different recensions and text-types, although this conception has lost its raison d'être, or, it needs at least to be newly and convincingly demonstrated.[29]
[56] In 2006, Holger Strutwolf, current director of the INTF, “advanced the view that it is time to abandon the concept of text-types altogether.”[30]
[57] The map and dendrogram presented here imply that textual clusters are real, although they differ from the three or four clearly defined text-types employed by earlier generations to describe the New Testament textual tradition. Rather than abandon the concept of text-types altogether, we should align our understanding with the reality, which is that New Testament textual clusters are hard to delineate but nevertheless exist. Epp provides a suitable analogy for their nebulous nature:
A text-type is not a closely concentrated entity with rigid boundaries, but is more like a galaxy — with a compact nucleus and additional but less closely related members which range out from the nucleus toward the perimeter. An obvious problem is how to determine when the outer limits of those more remote, accompanying members have been reached for one text-type and where the next begins.[31]
[58] Being the result of an objective analytical procedure, a dendrogram generated by divisive clustering should be a better approximation of the textual reality than the conventional system of text-types. However, using a partitioned dendrogram presents the immediate challenge of what to name each cluster. One possibility is to apply a label to each, perhaps based on a supposed geographic association or leading members of the relevant cluster; another is to enumerate each member; yet another orders the members of each cluster in some way then gives the first and last separated by an ellipsis. Hopefully, whichever approach prevails will not lead to a profusion of different names for the same clusters. In what follows, I will identify each cluster with its first and last members as ordered in the dendrogram.
[59] The dendrogram has a self-similar character whereby each subtree has a similar appearance to the whole. A subtree can itself be partitioned by chopping at some height. Thus, the great cloud of witnesses which make up the fourth cluster of the six-way partition (i.e. K, L, P, and the rest) can be divided into seven by cutting at a height of 0.4:
K ... 1319
104 ... 263
365 ... slav
geo-2
075
eth-pp, eth-TH
P ... 044
[60] Although some details of this partition would probably change if a larger sample was analysed, what is seen here serves as a starting point for discussion. The fourth, fifth, and sixth clusters are solitary, having only one or two members among the sampled witnesses. Nevertheless, they are kindred to the other witnesses in this great cloud. With one possible exception, all of the remaining clusters have been identified before: the K ... 1319 cluster is associated with the Byzantine standard text which became dominant after the fourth century; Waltz lists five members of the 104 ... 263 cluster under his “family 2127,” noting that some belong to von Soden's Ia3 group in Paul;[32] as for the P ... 044 cluster, MDS maps produced during my doctoral research reveal that P, 044, and 0150 are neighbours.[33] Concerning the possible exception, I don't know whether anyone has previously noticed a similarity between 365, 1912, and the Greek text presumed to stand behind the Old Church Slavonic version.
[61] It is natural to ask what each cluster represents and how the overall picture came to have its present form. If it was possible to produce a sequence of maps showing the distribution of witnesses in textual space at the end of each year for the first few centuries of textual transmission, I imagine that animating the sequence would result in what looks like an exploding firework whose initial burst gives rise to a series of other bursts which in turn gives rise to yet more bursts, and so on, expanding ever outwards. If this is a good analogy, what agents are to blame for driving the fragments apart? The culprits are the copyists.
[62] Whether by chance or design, copyists introduced novel readings. Once there was a choice of readings, copyists began to choose among those that were already known in their sphere. It seems that typical copyists preferred to choose among existing readings rather than to create novel ones. This is not to say that a copyist would never amend the exemplar's text, especially when faced with an apparent difficulty or corruption. However, there is evidence to suggest that normal practice was to choose among existing readings. For example, the UBS4 apparatus of Hebrews shows that the number of readings in a variation unit follows a certain pattern:
| Readings | Variation units |
|---|---|
| 2 | 24 |
| 3 | 9 |
| 4 | 7 |
| 5 | 2 |
| 6 | 2 |
| > 6 | 0 |
[63] Here, the number of readings in a variation unit is usually two, perhaps three or four, but seldom more. If copyists were creating new readings all the time then one would expect the frequency of variation units with more than a few readings to be greater.[34]
[64] Given that the main outcome of the copying process was to reproduce known readings, what determined which ones would be chosen at a particular place and time? If readings had a high mobility then copyists in far flung places would be aware of them and so be able to select them in preference to others. These “viral” readings would then spread throughout the population of texts with ease. If, on the other hand, readings were not so mobile then the preponderance of those available for selection would be local ones. If this was the case then one would expect geographically localised species of text to arise. Regardless of the mobility of readings, the particular reading chosen when the copyist knew there were alternatives was a matter of scribal psychology: whatever reading was best adapted to be selected by the scribe had the best chance of being reproduced.
[65] The question of whether local texts were likely to form during a particular phase of textual history then comes down to the question of how mobile readings were at the time. This, in turn, rests on the question of how mobile the vectors of the viral readings were, namely the manuscripts.[35] Epp shows that during the first few centuries of the Christian era, letters and documents could be transported far and wide with surprising speed.[36] Nevertheless, I suggest that the principle of least effort, which is useful for understanding many human enterprises, would make it preferable to pick up a nearby exemplar rather than send for an exotic one when a copy had to be made.[37]
[66] What then? Were manuscripts so mobile as to make the development of local texts unlikely? It seems that MDS maps provide a clue and at the same time give us reason to revisit a theory of the text which has fallen out of favour. The following figure shows a two-dimensional projection of the classical MDS result obtained from the Hebrews data:
[67] Strangely enough, there seems to be a correspondence between this map and a physical map of the Mediterranean:[38]
[68] A number of broad correlations between textual clusters and early Christian population centres emerge when the MDS and physical maps are compared:
Members of the “Western” cluster (e.g. Old Latins and Vulgate) are to the west.
A great cloud of witnesses spreads across an arc encompassing the north-eastern and eastern shores of the Mediterranean. This cloud includes a number of witnesses whose textual locations correspond to their suspected geographical provenances, such as Chrysostom, the Byzantine standard text, and the Syriac versions.
The “secondary Alexandrian” cluster (A, C, 33, etc.) corresponds to Egypt.
[69] If the correlation between textual clusters in MDS maps and physical locations of Christian population centres around the Mediterranean rim is more than coincidental then MDS maps can be used to associate textual clusters with geographical locations. One can then speculate that the “southern” part of the great cloud should be associated with Palestine, and begin to remember something said long ago by B. H. Streeter:
If we look at the map we see at once that the Churches whose early texts we have attempted to identify stand in a circle round the Eastern Mediterranean — Alexandria, Caesarea, Antioch, (Ephesus), Italy-Gaul, and Carthage. The remarkable thing is that the texts we have examined form, as it were, a graded series. Each member of the series has many readings peculiar to itself, but each is related to its next-door neighbour far more closely than to remoter members of the series... Antecedently we should rather expect the text of any particular locality to be, up to a point, intermediate between those of localities geographically contiguous with it on either side. But the exactness of correspondence between the geographical propinquity and the resemblance of text exceeds anything we should have anticipated.[39]
[70] Whereas his work on the synoptic problem remains foundational, Streeter's theory of local texts seems to have fallen by the wayside. As Metzger and Ehrman say,
Today, there are few critics who follow Streeter's method in all of its particulars. Most recognize that the Caesarean text, for example, cannot be firmly established ... and that, in fact, apart from the text of Alexandria, it is difficult to find clearly demarcated textual families associated with the various major sees of early Christendom.[40]
[71] Does Streeter's theory of local texts deserve to be shelved? Even though his postulated “Caesarean” text-type seems to have disintegrated, his expectation of an association between textual complexion and geographical locality seems to be supported by the MDS maps.[41]
[72] These maps have some puzzling features, however. For instance, why is the Ethiopic in the “north-eastern” region? Why is the Armenian in the “secondary Alexandrian” cluster? And what about P46 and B? The location of the Ethiopic is not too hard to explain once it is remembered that there were historical connections between the Syrian and Ethiopian churches. The location of the Armenian suggests that it was revised against a secondary Alexandrian model. Streeter anticipated this, although he thought the revisers' model was a “Caesarean” rather than “Alexandrian” text. Speaking of the fifty Bibles commissioned by Constantine from Eusebius, whose texts might be expected to be like those current in Caesarea at the time, he wrote:
Thus many of the fifty copies originally made for Constantinople, more of less corrected to the standard [i.e. Byzantine] text, would get into the provinces... I venture the suggestion that one of these discarded MSS. was used by St. Mesrop and St. Sahak to revise the Armenian version.[42]
[73] Could it be that the “secondary Alexandrian” cluster contains witnesses descended from Constantine's fifty? Such a monumental event in textual history as the production of those fifty might be expected to have left a mark on the tradition, and the MDS map may be revealing its echoes here.
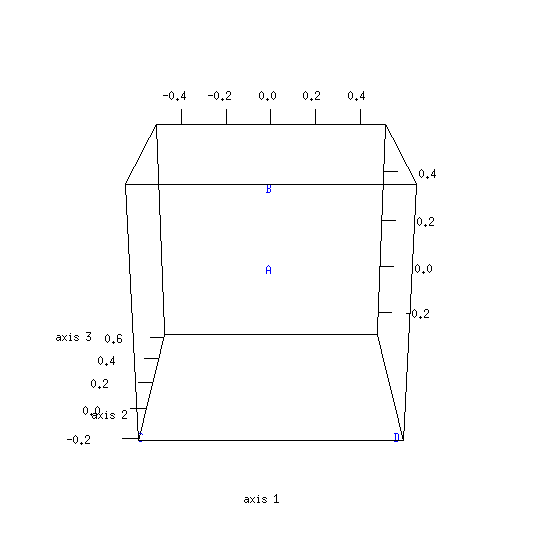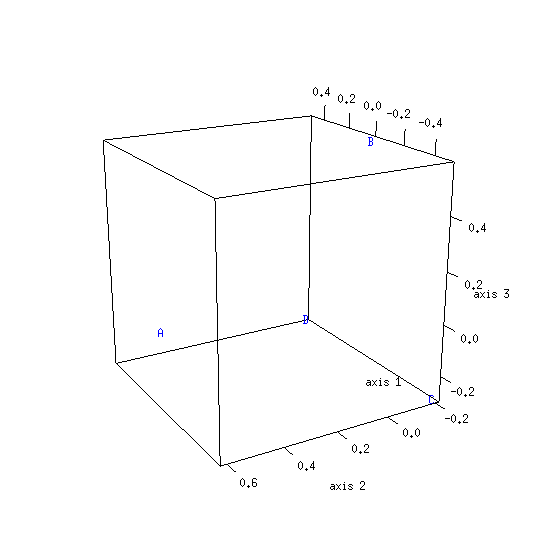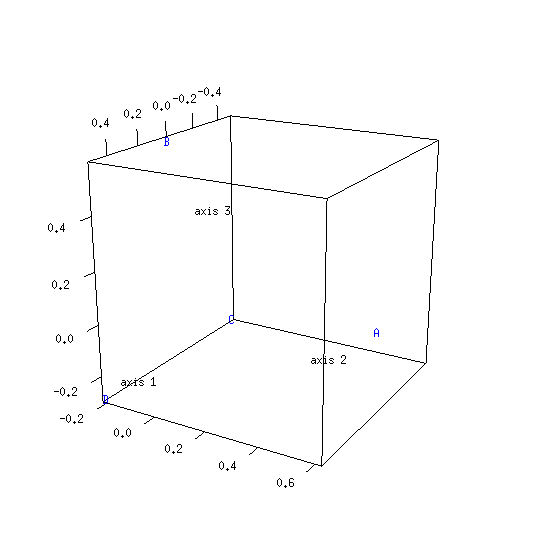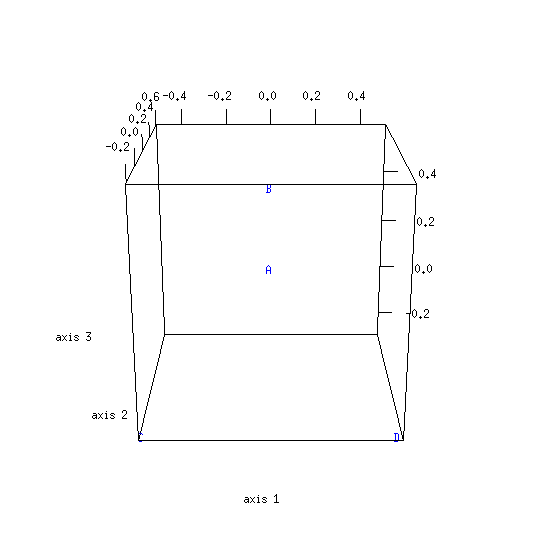
[74] Until now nothing has been said about the textual locations of P46 and B (Codex Vaticanus), the first being our oldest and the second, so some would say, best witness to the “original” text. Looking at the particular projection shown in the preceding MDS map would suggest that B should be associated with a location far to the east of any Christian population centre that flourished in the first two centuries after Christ. Furthermore, P46 would be associated with Palestine or Syria. Surely something is wrong! Taking another two-dimensional projection of the three-dimensional map resolves these difficulties:
[75] Now a geographical interpretation would place the texts of P46 and B in their own locality to the west of the rest: P46 might even be associated with Italy and B could be interpreted as a text with Italian and African ancestry. The Old Latin and Vulgate texts would be associated with the western side of the north-eastern region. Asia Minor fits this description, a possibility which was again anticipated by Streeter when he said, “there is a certain amount of evidence that in the second century the text used at Ephesus was akin to that found in ... the European Latin.” [43] Whether the Old Latins go back to a particular geographical location or locations is unknown, and it may be that a study which applies multivariate analysis to the Latin manuscript tradition will throw light on the subject.
[76] Perhaps P46 preserves an Italian text?[44] This manuscript is almost unique in placing the Letter to the Hebrews immediately after the Letter to the Romans. Trobisch explains the unusual placement by reference to the lengths of the writings in the Pauline corpus. However, if the Letter to the Hebrews was originally addressed to Rome and was subsequently broadcast from there, one can imagine that an Italian copyist would give Hebrews pride of place in a copy which eventually gave rise to descendants such as P46.[45]
[77] The MDS maps are food for thought. A geographical interpretation, which is inherently two-dimensional, cannot be pressed too far given that two- or even three-dimensional representations account for less than half of the distance information contained in a typical apparatus. Furthermore, it may be that another factor such as organizational structure within the early church was more influential in determining which channels of textual transmission would predominate. Even so, these MDS maps provide a clue that the textual space occupied by New Testament witnesses has been shaped by geographical forces.
[78] A final question remains. Where would the “original” text be located? Epp warns that the term “original” is multivalent (i.e. has multiple meanings) when used in relation to the New Testament text:
The issue of “original text” is, for example, more complex than the issue of canon, because the former includes questions of both canon and authority. It is more complex than possessing Greek gospels when Jesus spoke primarily Aramaic, because the transmission of traditions in different languages and their translation from one to another are relevant factors in what is “original.” It is more complex than matters of oral tradition and form criticism, because “original text” encompasses aspects of the formation and transmission of pre-literary New Testament tradition. It is more complex than the Synoptic problem and other questions of compositional stages within and behind the New Testament, because such matters affect definitions of authorship, and of the origin and unity of writings. More directly, it is more complex than making a textual decision in a variation unit containing multiple readings when no “original” is readily discernible, because the issue is broader and richer than merely choosing a single “original” and even allows making no choice at all. Finally, what “original text” signifies is more complex than Hermann von Soden's, or Westcott-Hort's, or any other system of text types, or B. H. Streeter's theory of local texts, or various current text-critical methodologies, including the criteria for originality of readings, or “rigorous” versus “reasoned” eclecticisms, or claims of theological tendencies or idealogical alterations of readings and manuscripts, because the question of “original text” encompasses all of these and much more.[46]
[79] In a more recent article, Epp advocates a “variant-conscious” edition of the Greek New Testament where the variants are “in your face” instead of hidden in the apparatus.[47] Rather than this treasury of readings approach, the INTF still seeks to reconstruct a single entity called the “initial” text which Mink describes in the following terms:
The initial text is a hypothetical, reconstructed text, as it presumably existed, according to the hypothesis, before the beginning of its copying. In a hypothesis, which wants to establish the genealogical relationship between the witnesses, the initial text corresponds to a hypothetical witness A ('Ausgangstext'). The initial text is not identical with the original, the text of the author. Between the autograph and the initial text, considerable changes may have taken place which may not have left a single trace in the surviving textual tradition. Even if this is not the case, differences between the original and the initial text must be taken into account.
On the other hand, the initial text is not simply a reconstruction on the basis of surviving variants, which best explains the emergence of the variants and thus represents the archetype of the tradition. Instead, several hypotheses are possible about the beginnings of the tradition. The simplest working hypothesis must be that there are no differences between the original and the initial text (except for inevitable scribal slips). In that case, the reconstruction of the initial text is not only determined by the subsequent tradition (which text form could have been derived from which?), but also by the author's intentions as they come to light in the totality of what we know about him (is a variant more likely to come from the pen of the author or from a copyist?). Another possible hypothesis might involve an editor in-between the author and the initial text, who might possibly have merged several writings of an author into one. Or there may have been more than one initial text, possibly even going back to more than one autograph if, for example, the author issued several versions of his work.[48]
[80] In the case of the Letter to the Hebrews, we have a text that does not show any signs of major textual dislocation as far as the extant witnesses are concerned. It seems to descend from a single exemplar, a copy of which was incorporated into a collection of Paul's letters.[49] If the Letter to the Hebrews was sent to Rome then broadcast from there as part of a collection, the initial copy could have been made directly from the original. What is more, the collection could have been in codex form from the outset. Zuntz dates publication of the collection around the end of the first century.[50] By this time, according to Bagnall, the codex form was already being used for books in Rome:
Many authors have in fact noticed that the case for the Roman origin of the codex is strong, even decisive. Our first good evidence of its use for books (as opposed to private notes and memoranda, written on wooden tablets strung together) comes from first-century Rome.[51]
[81] Returning to the analogy of a firework, the initial text rocketing up and about to explode is, then, a copy of Hebrews carried in a collection of Paul's letters, perhaps launched from Rome around the end of the first century in codex form. If the picture we now see represents primordial copies dispersed to early Christian population centres at that time, how should we seek to recover the initial text? It may be that the best approach is to remain agnostic concerning where the initial text came from and to distill the text represented by each cluster then use these “hyparchetypes” to approach the initial text. Alternatively, we could choose one place as the most likely initial distribution centre for the collection of Paul's letters then seek the initial text from those witnesses which preserve its local text. If that place was Rome then the MDS maps taken together with a geographical interpretation hint that the texts of P46 and B are the closest surviving relatives of the initial text of Hebrews.
[1] Barbara Aland, Kurt Aland, Johannes Karavidopoulos, Carlo M. Martini, and Bruce M. Metzger, eds, The Greek New Testament, (4th rev. ed.; Stuttgart: Deutsche Bibelgesellschaft, 1993).
[2] Barbara Aland, Kurt Aland, Johannes Karavidopoulos, Carlo M. Martini, and Bruce M. Metzger, eds, Novum Testamentum Graece (27th rev. ed.; Stuttgart: Deutsche Bibelgesellschaft, 1993).
[3] These represent a summary of the readings. One manuscript (P46) has αὐτοῦ instead of ἑαυτοῦ for the second reading while some witnesses have αὑτοῦ or αὐτοῦ instead of ἑαυτοῦ for the third.
[5] A comparison on the basis of order might be meaningful for a data matrix constructed from the UBS4 apparatus because the editors always place their preferred reading first.
[6] Provided that certain mathematical conditions are met, a dissimilarity can be called a distance. Other dissimilarity measures exist but not all are suitable for nominal data.
[7] The original text of Codex Vaticanus (B) is missing from Heb 9:14 to the end, explaining in large part why there are only 23 out of 44 variation units where the readings of both P46 and B are defined. (The reading of P46 is undefined at two of the 44 variation units.) Distances are quoted to three significant figures regardless of whether this level of precision is warranted. Being a ratio of two counts, the simple matching distance is a dimensionless quantity; it is a pure number with no unit.
[8] These were generated using the R statistical computing
environment. (See The R Project for Statistical Computing at
http://www.r-project.org/.) The
following statement was executed twice to obtain the random numerals: rbinom(10,
1, 0.5).
[9] This equation employs factorial notation, where n! = n x (n - 1) x ... x 2 x 1. P(k) is the probability of k out of n disagreements and p is the probability of disagreement, which is the complement of the probability of agreement. That is, P(disagreement) = p and P(agreement) = 1 - p, where “P(x)” stands for “probability of x.”
[10] Using R, critical limits for a binomial distribution can be
calculated with the expression qbinom(c(0.025, 0.975), n, p), where n is
the number of trials and p the probability of success. In this case, the
alpha level of 0.05 is split between the two tails,
resulting in cumulative probabilities of 0.025 and 0.975. There are ten trials, each
with a probability of success equal to one half (0.5).
[11] The usefulness of such an estimate is questionable. The extant evidence may not be representative of all phases of textual development. Furthermore, a multiplicity of similar witnesses, such as those with the Byzantine standard text, can skew the result. Fortunately, the UBS4 apparatus subsumes most Byzantine witnesses under a single group symbol, thereby alleviating this problem.
[12] These critical limits were calculated using an R script written for the purpose. All of the scripts employed to derive results for this article are available upon request. As it happens, the same critical limits are obtained using the binomial distribution with a probability of disagreement equal to the mean probability of disagreement taken across the 23 variation units. Chapter three of Timothy J. Finney, Analysis of Textual Variation, http://purl.org/tfinney/ATV/, provides a comparison of results obtained by binomial, exact, and Monte Carlo calculations.
[13] Various refinements have been made to the definition of a variation unit. See, for example, those by Ernest C. Colwell and Ernest W. Tune, “Method in Classifying and Evaluating Variant Readings” in Studies in Methodology in Textual Criticism of the New Testament (New Testament Tools and Studies 9; Leiden: Brill, 1969) 98-9; Eldon J. Epp, “Toward the Clarification of the Term 'Textual Variant'” in Studies in the Theory and Method of New Testament Textual Criticism (ed. Eldon J. Epp and Gordon D. Fee; Studies and Documents 45; Grand Rapids: Eerdmans) 60-1; and Gordon D. Fee, “On the Types, Classification, and Presentation of Textual Variation” in Studies in the Theory and Method, 62-6.
[14] Aland, Barbara, Kurt Aland†, Gerd Mink, Holger Strutwolf, and Klaus Wachtel, eds, Novum Testamentum Graecum Editio Critica Maior: IV: Catholic Letters (Stuttgart: Deutsche Bibelgesellschaft, 1997-). Dr Klaus Wachtel of the INTF kindly supplied the number of variation units.
[15] There is no guarantee that the interval will contain the actual distance for a given sample: the actual value is either inside or outside the calculated confidence interval. One cannot be sure that a confidence interval contains the actual value unless the entire population is examined.
[16] See David S. Moore and George P. McCabe, Introduction to the Practice of Statistics (2nd ed.; New York: Freeman, 1993) 372-4. There are four conditions: (1) a fixed number of observations; (2) the observations are independent; (3) there are only two possible outcomes for each observation; and (4) the probability of a “success” (i.e. disagreement) is the same for each observation. The last condition is approximately true if the population size is much larger than the sample size.
[17] These limits can be obtained using the R expression
qbinom(c(0.025, 0.975), 23, 3/23).
[18] Moore and McCabe, Introduction, 582.
[19] These were selected from the output of an R script written to estimate relative interval widths for a range of sample sizes. The relative width is obtained by dividing the number of distinct counts in the interval by the total number of possible counts. For example, the limits of the confidence interval for a sample size of fifteen are 4 and 11, representing eight distinct counts (i.e. 4, 5, 6, ..., 9, 10, 11). As there are sixteen possible counts (i.e. 0, 1, 2, ..., 13, 14, 15), the relative width of the interval is 8/16 or 50%.
[20] The 54 objects are comprised of 53 witnesses and the object representing the UBS text.
The constraint upon the minimum sample size requires that all pairs of witnesses share at
least twelve variation units where the readings of both are defined (i.e. are not marked
as indeterminate using NA). Witnesses that do not satisfy the constraint are
dropped using the following algorithm:
Eliminate from the data matrix all witnesses defined in less than the required number of variation units.
Construct a table that records the number of shared variation units in which both witnesses are defined for each pair of remaining witnesses.
For each pair with an insufficient number, eliminate from the data matrix that witness with the least number of shared and defined variation units taken across all remaining witnesses.
Repeat the second and third steps until no pairs with an insufficient number remain.
[21] W. N. Venables and B. D. Ripley, Modern Applied Statistics with S (4th ed.; New York: Springer, 2002) 306.
[22] Christopher Chatfield and Alexander J. Collins, Introduction to Multivariate Analysis (London: Chapman and Hall, 1980) 212.
[23] Ibid., 216.
[24] The “Divisive Coefficient” indicates the degree of clustering in the data.
[25] Divisive clustering only considers the distances between witnesses and does not take account of genealogical information. The resulting chart is not a genealogical tree as would be produced by phylogenetic analysis. Instead, it is a chart that indicates how the group of all witnesses divides into subgroups when the divisive clustering procedure is applied. Details of this procedure are given in the associated documentation accessible through the R statistical environment. For a good example of a phylogenetic analysis relating to New Testament witnesses, see Matthew Spencer, Klaus Wachtel, and Christopher J. Howe, “The Greek Vorlage of the Syra Harclensis: A Comparative Study on Method in Exploring Textual Genealogy,” TC: A Journal of Textual Criticism 7 (2002) http://purl.org/TC/vol07/SWH2002/. The “coherence-based genealogical method” developed by the INTF also uses genealogical information: see Gerd Mink, “Problems of a Highly Contaminated Tradition: The New Testament: Stemmata of Variants as a Source of a Genealogy for Witnesses,” in Studies in Stemmatology II (ed. P. van Reenan, A. den Hollander, and M. van Mulken; Amsterdam: John Benjamins, 2004) 13-85, for an explanation of this method. As an adjunct, the INTF has developed a Genealogical Queries program which provides access to a database developed in conjunction with their ECM: see Klaus Wachtel and Volker Krüger, “Genealogical Queries,” http://intf.uni-muenster.de/cbgm2/en.html.
[26] Chatfield and Collins, Introduction to Multivariate Analysis, 213, 220. A dendrogram that does imply a natural partition has long “branches” tipped by compact bunches of “leaves;” that is, within-cluster distances tend to be small when compared with between-cluster distances.
[27] See Bruce M. Metzger and Bart D. Ehrman, The Text of the New Testament: Its Transmission, Corruption, and Restoration (4th ed.; New York: Oxford University Press, 2005) 306-13, for a convenient summary of these text-types.
[28] Robert B. Waltz, “Family 1739,” http://www.skypoint.com/members/waltzmn/Manuscripts1501-2000.html#fam1739.
[29] Kurt Aland, “The Significance of the Papyri for Progress in New Testament Research” in The Bible in Modern Scholarship (ed. J. P. Hyatt; Nashville: Abingdon Press, 1965) 336-7.
[30] D. C. Parker, An Introduction to the New Testament Manuscripts and their Texts (Cambridge: Cambridge University Press, 2008) 174.
[31] Eldon J. Epp, “The Significance of the Papyri for Determining the Nature of the New Testament Text in the Second Century: A Dynamic View of Textual Transmission” in Gospel Traditions in the Second Century: Origins, Recensions, Text, and Transmission (Christianity and Judaism in Antiquity 3; Notre Dame: University of Notre Dame Press, 1989) 95.
[32] Robert B. Waltz, “Text Types And Textual Kinship,” http://www.skypoint.com/members/waltzmn/TextTypes.html. The note which lists members of his family 2127 is found in “Appendix II: Text-Types and their Witnesses.” The link with von Soden's Ia3 is noted in “Appendix III: Von Soden's Textual System.”
[33] The association is evident from textual maps of 044 in Timothy J. Finney, "The Ancient Witnesses of the Epistle to the Hebrews" (PhD diss., Murdoch University, Western Australia, 1999) http://purl.org/tfinney/PhD/PDF/part3.pdf, 124. According to the dendrogram shown above, the Harclean Syriac (syr-h) also belongs in this cluster. The circumstances surrounding this revision of the Syriac are known; it was produced by Thomas of Harkel who consulted Greek manuscripts during its production around 616 C.E. at Enaton monastery near Alexandria. Perhaps the Greek witnesses which the dendrogram places near the Harclean Syriac (i.e. P, 044, and 0150) represent a variety of the text that was prevalent in monastic Egypt at the time?
[34] The UBS4 apparatus sometimes reduces the number of readings in a variation unit by lumping similar ones together. Even if the full range of readings is reported, it remains true that a typical variation unit does not have many readings once orthographic differences are levelled. Graphs by Mink, “Problems of a Highly Contaminated Tradition,” 20, confirm that the same kind of relationship between frequency and number of readings is observed for the variation units examined during preparation of the ECM fascicles for James.
[35] Copyists and readers could also act as vectors, having memorised parts of the text.
[36] Eldon J. Epp, “New Testament Papyrus Manuscripts and Letter Carrying in Greco-Roman Times” in The Future of Early Christianity: Essays in Honor of Helmut Koester (ed. B. A. Pearson; Minneapolis: Fortress, 1991) 35-56.
[37] This is not to say copyists were lazy, just efficient. George K. Zipf, in Human Behavior and the Principle of Least Effort: An Introduction to Human Ecology (New York: Addison-Wesley, 1949), used the principle of least effort to explain many phenomena, including income distribution, city sizes, and word frequencies.
[38] This map by Adolf Harnack is titled “The Spread of Christianity down to 180 A.D.” and is found in his Mission and Expansion of Christianity in the First Three Centuries (2nd ed.; trans. and ed. James Moffatt; 2 vols; New York: G. P. Putnam's Sons, 1908). It has entered the public domain.
[39] Burnett Hillman Streeter, The Four Gospels: A Study of Origins, The Manuscript Tradition, Sources, Authorship, & Dates (London: Macmillan, 1924) 106. Propinquity means nearness.
[40] Metzger and Ehrman, Text of the New Testament, 218.
[41] Bruce M. Metzger, “The Caesarean Text of the Gospels” in Chapters in the History of New Testament Textual Criticism (New Testament Tools and Studies 4; Grand Rapids: Eerdmans, 1963) 67, writes, “By way of summary, it must be acknowledged that the Caesarean text is disintegrating.” Larry W. Hurtado, Text-Critical Methodology and the Pre-Caesarean Text: Codex W in the Gospel of Mark (Studies and Documents 43; Grand Rapids: Eerdmans, 1981) 88, suggests that the text represented by ϴ and its allies “is a form of Western text as it was shaped in the East.”
[42] Streeter, The Four Gospels, 104.
[43] Ibid., 69-70.
[44] Chapter five of my Analysis of Textual Variation includes classical MDS maps derived from the UBS4 apparatus of Hebrews which place Ambrose of Milan's text and the Old Latin it-r near P46.
[45] Frederic G. Kenyon, The Chester Beatty Biblical Papyri: Descriptions and Texts of Twelve Manuscripts on Papyrus of the Greek Bible: Fasciculus III Supplement: Pauline Epistles: Text (London: Emery Walker, 1936) xi, thought one other witness (minuscule 1919) placed Hebrews after Romans but noted that “There is some obscurity about this.” See David Trobisch, “The Oldest Extant Editions of the Letters of Paul” Religion Online (1999) http://www.religion-online.org/showarticle.asp?title=91, for his reasoning concerning the order of writings in P46. According to Craig R. Koester, Hebrews: A New Translation with Introduction and Commentary (Anchor Bible 36; New York: Doubleday, 2001) 48, “Speculation about the location of the addressees has produced many proposals. Jerusalem and Rome are the most common, with Rome currently deemed the most plausible.”
[46] Eldon J. Epp, “The Multivalence of the Term 'Original Text' in New Testament Textual Criticism” Harvard Theological Review 92 (1999) 246-7.
[47] Eldon J. Epp, “It's All About Variants: A Variant-Conscious Approach to New Testament Textual Criticism” Harvard Theological Review 100 (2007) 298.
[48] Mink, “Problems of a Highly Contaminated Tradition,” 25-6.
[49] Heb 13:22-25 might be a note appended by someone besides the author, although no extant witnesses omit this section as a block. In Hebrews, at least, we need not worry about the possibility of multiple originals. According to Trobisch, “Oldest Extant Editions,” “The uniformity of the title clearly demonstrates that all manuscripts of Hebrews go back to a single exemplar. In this exemplar Hebrews was already part of a collection of the letters of Paul.” Günther Zuntz, The Text of the Epistles: A Disquisition upon the Corpus Paulinum (Schweich Lectures, 1946; London: Oxford University Press, 1953) 14, writes that “The primitive Corpus Paulinum is the archetype which the recensio and examinatio of the extant evidence strive to recover.”
[50] Zuntz, Text of the Epistles, 14.
[51] Roger S. Bagnall, Early Christian Books in Egypt (Princeton: Princeton University Press, 2009) 86. Bagnall (ibid., 89) suggests that Christian use of the codex for their scripture derives from an authoritative centre, and notes that Roberts and Skeat had the same idea. He regards this centre to be the Roman church, something that Skeat also came to believe. Although Bagnall would place a later date on Christian adoption of the codex for scripture, it remains possible that Roman Christians used codices to distribute the Pauline collection from its inception.