Table of Contents
Multivariate analysis (MVA) can be applied to the New Testament textual tradition in order to investigate grouping among its witnesses. This article applies certain MVA methods to a number of example data sets. Each method operates on a matrix which tabulates distances between pairs of items in a data set. The simple matching distance, which is the proportion of disagreements, can be used as a metric for calculating distances between New Testament witnesses.
Analysis methods called classical multidimensional scaling (CMDS) and divisive clustering (DC) are useful for revealing group structure when it is well defined. However, they are less useful when grouping is not very distinct. A method called partitioning around medoids (PAM) provides another way to divide a data set into groups. Local maxima in a plot of a statistic called the mean silhouette width (MSW) indicate preferred numbers of groups.
Statistical analysis of a data set allows upper and lower critical limits to be defined for the distance between a pair of witnesses. Distances between these limits are not significant in the sense that the same range of distances is expected to occur for generated pairs whose states are randomly chosen from the available pool. Distances that are either less than or greater than these critical limits are not likely to happen by chance. A distance less than the lower critical limit indicates an adjacent relationship while one greater than the upper limit implies an opposite relationship.
Applying CMDS, DC, and PAM analysis to data for the Gospel of Mark reveals interesting features of the textual landscape. Witnesses tend to form groups which have points of contact with conventional categories such as the “Alexandrian,” “Byzantine,” “Western,” and “Eastern” types identified by prior generations of researchers. Multivariate analysis can also be used for novel purposes such as identifying group representatives, group cores, and readings useful for classification purposes.
Every book from antiquity which has survived in multiple copies exhibits textual variation. Sites where extant witnesses differ can be identified by manual or computer-assisted comparison. Once the state of every witness has been recorded at every variation site where its text is discernible, a text to text distance can be calculated for each pair of witnesses. Multivariate analysis of these distances provides a way to discover textual groups among the witnesses.
The boundaries of a variation site, the list of associated textual states, and the lists of witnesses that attest to the states constitute a structure called a variation unit. The boundaries of a variation site might be determined by a collation algorithm or through editorial discretion. Once the boundaries are defined, the alternative states of text found among the witnesses can be listed for that site. The term reading is often used to refer to the textual state of a witness. A reading may be classified as: substantive, affecting meaning; orthographic, affecting the surface form but not meaning; or erroneous, for clear blunders. A state which constitutes a substantive difference is often called a variant.
A compact structure called a data matrix is a
useful starting point for multivariate analysis of textual variation.[1] There is a row
for each witness, a column for each variation site, and a code representing which state
each witness preserves at each variation site where it is well defined. A distinct code
such as NA (not
available) is used when a witness is not well defined. There are various
reasons why this might be so: the witness could be illegible at the place in question or,
if a translation, might support more than one of the alternative states in the original
language.
A data matrix contains the information required to construct a second structure called a distance matrix using some metric to record the dissimilarity of every pair of witnesses being examined. One suitable metric, the simple matching distance (SMD), is the relative frequency of disagreement between two witnesses. Given a set of variation sites where both witnesses have well defined readings, the SMD is calculated by counting the number of disagreements and dividing by the number of sites. The resulting distance is dimensionless, having no unit, because it is the ratio of two pure numbers. Its magnitude varies from a minimum of zero for perfect agreement to a maximum of one for perfect disagreement.
To keep sampling error below a tolerable level, it is advisable to impose a constraint whereby witnesses are eliminated from the distance matrix if their inclusion would result in any distance being calculated from less than a minimum acceptable number of variation units where the states of both members of a pair are well defined. Witnesses whose inclusion would violate this constraint can be eliminated by an iterative procedure which drops the least well defined witness at every step until all remaining witnesses satisfy the constraint.
The textual landscape can be explored by applying multivariate analysis techniques such as classical multidimensional scaling (CMDS) and divisive clustering (DC) to a distance matrix. Also, statistical analysis of a distance matrix allows one to establish what range of distances between witnesses is expected to occur by chance, thereby providing a criterion for deciding whether two witnesses share a significant level of agreement. Although useful, these techniques are not always suitable for indicating how many groups exist, especially when grouping is not well defined. Another mode of multivariate analysis called partitioning around medoids (PAM) provides a robust way to divide a set of witnesses into a chosen number of groups. A statistic called the mean silhouette width (MSW), which can be generated during PAM analysis, indicates how many groups are in the data.
Four examples will be used to introduce a number of multivariate analysis techniques which can be used to explore grouping:
-
actual distances between thirty cities
-
an artificial construct which contains four well defined groups of three items each
-
textual variants in the Gospel of Mark extracted from the apparatus of the fourth edition of the United Bible Societies Greek New Testament (UBS4)
-
textual variants in the Gospel of Mark compiled by the Institut für Neutestamentliche Textforschung (INTF) as part of ongoing work on their Editio Critica Maior series.
This article uses the word case as a generic term for a member of a data set. In the first example, cases are cities; in the two examples based on New Testament textual data, they are witnesses.
Knowing what something is not can help one recognise the real thing. For this reason, the last three examples are complemented by controls comprised of randomly generated cases which are consequently unrelated. The same analysis techniques are applied to both primary and control examples so that results obtained for the primary examples can be contrasted with results obtained when there are no groups.
The distance matrix of the first example records distances between thirty busy airports identified by their IATA codes. As with all matrices in this article, this one can be downloaded as a comma-separated vector (CSV) file by clicking on the corresponding arrow symbol. Once downloaded, it can be imported into a spreadsheet program for inspection. The distances of this example were obtained with a formula that calculates tunnel distances from latitude and longitude coordinates. The formula is only accurate to 0.5% because the earth is not a perfect sphere. Resulting distances are rounded to the nearest kilometre.
This distance matrix has a number of characteristic features common to all distance matrices of the kind employed in this article:
-
it is square, having the same number of rows and columns, with one row and column per case (i.e. city in this example)
-
it is symmetrical because the distance from any case A to another case B is the same as the distance from B to A
-
its diagonal is comprised entirely of zeros because the distance from any case to itself is zero.
Classical multidimensional scaling (CMDS) produces a geometrical construct where cases are represented as points in a space. The procedure uses a least squares method to minimise differences between actual distances, as found in the distance matrix, and corresponding distances between points of the construct. The result is the best representation achievable using the available number of dimensions and chosen method of minimising differences. Achieving a perfect spatial representation of a distance matrix may require any number of dimensions up to one less than the number of cases. A coefficient called the proportion of variance indicates how well the construct reproduces the actual distances. It ranges from zero to one, with one indicating a perfect representation.
The CMDS map obtained by analysis of the first example's distance matrix seems to chart an alien world. Compared to a conventional globe, the construct is reflected and rotates around a different axis. This is not unexpected as the distance matrix contains no information concerning orientation or reflection. The proportion of variance coefficient has a value of 1.00, meaning that the map perfectly represents the distance matrix. If three dimensions had not been sufficient to reproduce all of the information in the distance matrix then the coefficient would have been less than one. In this case three dimensions is sufficient because the original distances relate to a three-dimensional world. The axis scales also conform to the data set, with the distance between opposite points (e.g. Singapore and Miami) corresponding to the Earth's diameter of approximately 12,750 km.
Divisive clustering (DC) begins with a single group and ends with individual cases. The relevant program documentation describes the clustering algorithm as follows, where observation refers to a case:[2]
At each stage, the cluster with the largest diameter is selected. (The diameter of a cluster is the largest dissimilarity between any two of its observations.) To divide the selected cluster, the algorithm first looks for its most disparate observation (i.e., which has the largest average dissimilarity to the other observations of the selected cluster). This observation initiates the "splinter group". In subsequent steps, the algorithm reassigns observations that are closer to the "splinter group" than to the "old party". The result is a division of the selected cluster into two new clusters.
Divisive clustering analysis produces a dendrogram which shows “heights” at which groups divide into sub-groups. The associated divisive coefficient ranges from zero to one, with larger values indicating more clearly defined grouping. A DC dendrogram is not a genealogical tree of the type produced by phylogenetic analysis. Instead, it merely shows a reasonable way to progressively subdivide an all-encompassing group until every sub-group is comprised of a single case.[3]
The DC dendrogram for the first example splits at a “height” of just over 12,000 kilometres, corresponding to the diameter of the entire point cloud. The left-hand branch splits into North American and European groups at a height of about 9,000 km which is the approximate distance between the centres of these two groups of cities. The North American group splits into eastern and western branches at a height of about 4,000 km, corresponding to the width of the continental USA. Sydney (SYD) and Dubai (DXB) are the first to split from the right-hand branch due to their relative isolation. The remaining cities in this branch split into East and Southeast Asian branches at a height of about 5,500 km.
If a case is on the border between two groups then a slight change in the distance matrix can cause it to switch from one branch of the dendrogram to another. A case in point is Dubai, which is about half way between the European and Asian groups. If this city were somehow to migrate closer to Europe then its location in the dendrogram would eventually shift out of the Asian group into the European one.
The second example introduces two new elements: the data
matrix and the control data set.
A data matrix records the states of a set of cases for a set of variables. The data
matrices used here adopt a convention where rows relate to cases and columns relate to
variables. Each row records the state of a case for each variable where it is well
defined. If the data relates to textual variation then there is a row for each witness,
a column for each variation site, and the states are codes which represent alternative
readings or, in the case of substantive variation, variants. If the state of a case is
not well defined for a particular variable then it is given the code NA (not available).
This example's data matrix is an
artificial construct in which the states of fifteen binary variables (V1-V15) have been chosen to produce four well
defined groups among twelve cases (A1-A12), with three cases per group. A binary variable is one with only two
possible states, here represented by the symbols 1 and 2. Cases within a group are similar while those of differing
groups are dissimilar.
The corresponding distance matrix was produced using the simple matching distance (SMD) to quantify the dissimilarity of every pair of cases. In this and the following examples, the distance matrix is generated from the corresponding data matrix using a script written in a statistical programming language called R.[4] The simple matching distance is obtained by counting the number of disagreements between two cases and dividing by the number of places where they are compared. (Both cases must be defined at each place where they are compared.) As the states in this example have been chosen to produce well defined groups, within-group distances should be small relative to between-group distances. Inspecting the distance matrix confirms that this is so, with cases in the same group having a distance of 2/15 (0.133) while distances between cases in differing groups are either 6/15 (0.400) or 8/15 (0.533). Inspection also shows that the distance matrix has the previously mentioned characteristics of being square, symmetrical, and having a diagonal comprised entirely of zeros. As in all distance matrices based on the simple matching distance, every distance has a value in the range between zero, representing perfect agreement, and one, representing perfect disagreement.
The CMDS result for this distance matrix reveals the four well defined groups, placing dissimilar cases apart and similar ones together. The proportion of variance figure of 0.61 obtained during the analysis indicates that the three dimensions allowed for the analysis result are not sufficient to perfectly reproduce the actual distances. On one hand, the CMDS result represents the data set well, giving a useful indication of the distance between dissimilar groups. On the other hand, it hides differences between cases in the same group. The four groups occupy the apexes of a regular tetrahedron because each one is equidistant from the others, as determined in advance when the corresponding data matrix was constructed. Given a different number of artificial groups, the resulting map would present a different picture; if, say, there had been three groups, they would have occupied the apexes of a triangle.
The DC dendrogram produced from this distance matrix also reveals the four groups. An initial all-encompassing group decomposes into four groups at a height of 0.533, which is the most common distance between cases in dissimilar groups. Each group splits into individual items at a height of 0.133, which is the distance between cases in the same group. In this example, DC is better than CMDS with respect to indicating distances between cases in the same group. The dendrogram has the characteristic pattern produced by data with well defined groups: long “branches” tipped by tight bunches of “leaves.” The divisive coefficient associated with this dendrogram is 0.75.
The control data set is based on random data and shows what analysis results look like
in the absence of groups. The control data matrix was produced by a program which generates the required number of
cases by randomly selecting between two possible states for the required number of
variables.[5] Cases are labelled with an R prefixed
to a numeral, variables with a V prefix, and states as 1 and 2. The control data sets of the
following sections were produced by the same program and have the same labelling system.
Cases and variables from different controls are distinct even though their labels may
coincide.
The controls are intended to show what analysis results look like for a data set which is comparable to the primary example yet does not contain any real groups. The program which makes them is supplied with three parameters:
-
the required number of cases
-
the required number of variables
-
the desired mean distance between cases.
For each case produced, the program randomly selects a state for every variable in a manner that aims to produce the desired mean distance between cases. A distance matrix produced from the resulting data matrix will have approximately the same mean distance between cases as desired.[6] The data matrix of the present control was produced using parameters which correspond to the primary example: twelve cases, fifteen variables, and a desired mean distance between cases of 0.424.
The corresponding distance
matrix is again obtained by calculating the simple matching distance for every
pair of cases. The mean distance between the randomly generated cases is 0.481. While
this is some way off the desired value of 0.424, the difference is not unexpected given
that the cases were generated by a random process. As with all of the controls,
agreement between a pair of randomly generated cases is a purely random phenomenon.
Apart from having the same two states among which to choose for every variable, none of
these cases is related. In view of this, it may be surprising to find that some, such as
R4 and R8, are relatively close to
each other while others, such as R1 and R5, are relatively far apart. Due to the nature of random processes, if enough
random cases were produced then the distances between pairs would encompass the full
range of possible values, with a minimum of zero and a maximum of one. The frequencies
with which various distances occur would vary, extreme values being less common than
others.
The CMDS map of these unrelated cases is roughly spherical. There are variations in the density of cases across different volume elements within the space, but these are merely random fluctuations. This map illustrates an important point: random agreement can mimic group structure even when none actually exists. The proportion of variance coefficient is 0.65, meaning that the map conveys less than two-thirds of the information contained in the distance matrix. Nevertheless, this is still the best representation possible when the analysis is forced to work in only three dimensions. If more dimensions were allowed then more congruent results would follow. However, the problem remains of how to convey such results when our spatial perception is limited to three dimensions.
The corresponding DC dendrogram has a divisive coefficient of 0.51, not zero as might be expected but still a good deal less than the value of 0.75 obtained for the primary example. A dendrogram can be “cut” at a certain height to partition the cases into a number of groups. This is achieved by choosing a height, drawing a horizontal line across the dendrogram at that height, then grouping cases which belong to each sub-branch thus defined. Any height might be chosen, one possibility being the mean distance between pairs of cases. Cutting this dendrogram at a height equal to the mean distance of 0.481 produces the following partition:
Table 3. A partition of unrelated cases
| Cluster | Members |
|---|---|
| 1 | R1 R4 R8 R12 |
| 2 | R2 R3 R9 |
| 3 | R5 R7 R11 |
| 4 | R6 R10 |
This illustrates another important point: a method of analysis can be used to partition a data set even when its cases are unrelated. Cutting a dendrogram at some height can produce any number of groups between one and the total number of cases. At what height should a dendrogram be cut to produce groups where members are actually related? For this dendrogram, an appropriate height would be something less than 0.2, the minimum distance between these randomly generated cases. Cutting at such a height produces a more sensible partition with only a solitary case per group.
This example relates to textual variations in the Gospel of Mark as recorded in the
fourth edition of the United Bible Societies Greek New
Testament (UBS4).[7] Richard Mallett deserves thanks for performing the
exacting task of manually constructing the data matrix by encoding the variants found in the UBS4 apparatus.
The resulting matrix has 229 rows, one per witness, and 142 columns, one per variation
unit presented for the Gospel of Mark. A numeral is used to encode the variant supported
by a witness when its state is known at a variation site. If the state is not well
defined then the code NA is used. Minuscule 2427 has been left
in the data matrix even though it is now regarded as spurious. (Adding or omitting a
single witness seldom has much effect on results obtained by the analysis methods used
in this article.)
The corresponding distance matrix has only 65 rows and columns, one of each per witness which has survived the vetting process required to reduce sampling error to a tolerable level. The other 164 witnesses have been dropped because including any one of them would result in at least one distance being calculated by comparison of less than fifteen variation units where both members of a pair have a definite textual state. The mean distance between cases for this distance matrix is 0.471.
Subjecting this distance matrix to classical multidimensional scaling produces a map which may be described as tetrahedral, having three lobes of relatively high witness density diverging away from, or converging towards, a dense concentration of Byzantine witnesses. Regions between the three lobes are practically devoid of witnesses. At least in this data set, it is rare to find a text which lies between two non-Byzantine varieties. There are a few exceptions to this rule, including Old Latin Codex Bobbiensis (it-k) and Codex Koridethi (038): Bobbiensis stands about the same distance from what some would call “Western” and “Alexandrian” groups; Koridethi is between the “Western” group and a complex which includes the Sinaitic Syriac (syr-s), Armenian (arm), and Georgian (geo) versions. The proportion of variance figure for this map is 0.51, indicating that a three-dimensional treatment only conveys about half of the information contained in the distance matrix.
Divisive clustering analysis produces a dendrogram which, if cut at a height of 0.6, divides the witnesses into approximately the same groups as found in the CMDS map. However, the dendrogram might just as well be cut at another height to produce another number of groups. The associated divisive coefficient is 0.74. Its significance will not become apparent until compared with the divisive coefficient produced through DC analysis of a comparable distance matrix derived from random data.
The control data matrix was generated by the same program used to produce all of the controls in this article. Parameters supplied to the program are those required to produce a comparable distance matrix once it has been calculated from the generated data matrix. To be comparable, the generated data matrix needs to produce 65 cases with 142 variables per case while aiming for a mean distance between cases of 0.471.
The distance matrix calculated from the control data matrix turns out to have a mean distance between cases of 0.467. The distances between pairs of cases ranges from 0.338 to 0.613, excluding the distance of zero obtained when each case is compared with itself. This gives a sense of the normal range of distances to be expected for 65 unrelated cases of 142 variables each and a mean distance between cases of about 0.471.
Analysing this distance matrix to produce a CMDS map produces a spherical point cloud with a number of density fluctuations which might be misinterpreted as groups. This shows what kind of map to expect when a data set of this size and mean distance between cases contains no groups. Any apparent groups are spurious. The proportion of variance figure is 0.15, indicating that the map conveys less than one sixth of the information contained in the distance matrix. By contrast, the figure for the UBS4 data set is 0.51. Apparently, squeezing the distance information into three dimensions is far easier for the UBS4 data than for analogous random data.
At first glance, the DC dendrogram for the control is not unlike that of the primary example. There are a couple of significant differences, however. Firstly, the heights at which branches form ranges from 0.34 to 0.61, the same range found in the control distance matrix. By contrast, the range of heights in the dendrogram of the primary example is broader, varying between 0.008 and 0.86. Distances between the real cases tend to greater extremes than expected of data where states have been chosen at random. Sometimes the distances are smaller than normal, corresponding to a tendency for some witnesses to have similar sets of readings. Elsewhere the distances are larger than normal, consistent with a process which acted to drive certain texts apart. (Here, normal means what is expected of texts whose readings have been randomly selected from two possible states.) Secondly, the divisive coefficient for the control dendrogram is 0.34. Now the significance of the primary example's divisive coefficient of 0.74 can be appreciated. The magnitude of this grouping indicator is much greater for the UBS4 data set than for an analogous data set which has no groups. These numbers indicate that grouping among New Testament witnesses is a real phenomenon.
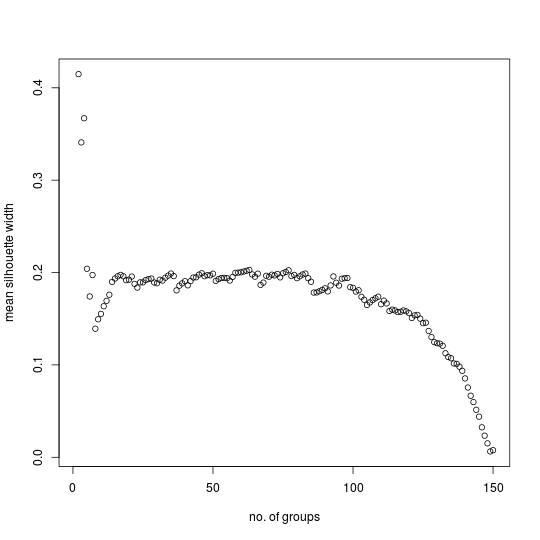
The fourth example is based on textual variation data collected by the INTF for the Parallel Pericopes installment of their Editio Critica Maior. The data matrix was generated from an electronic file made available by the INTF at their website. It records the states of 333 texts at 503 variation sites.[8] The corresponding distance matrix retains only 151 of those texts, the other 182 having been eliminated to reduce sampling error. Its distances range from 0.002 to 0.413 and have a mean value of 0.159.
Analysing this distance matrix produces a CMDS map with a similar appearance to the one obtained for the UBS4 data on Mark's Gospel. Both maps have three lobes of relatively high witness density diverging away from, or converging towards, a dense concentration of Byzantine witnesses. Once again, regions between the three non-Byzantine lobes are practically vacant. The proportion of variance figure for this map is only 0.32, implying that it accounts for less than one third of the information contained in the distance matrix.
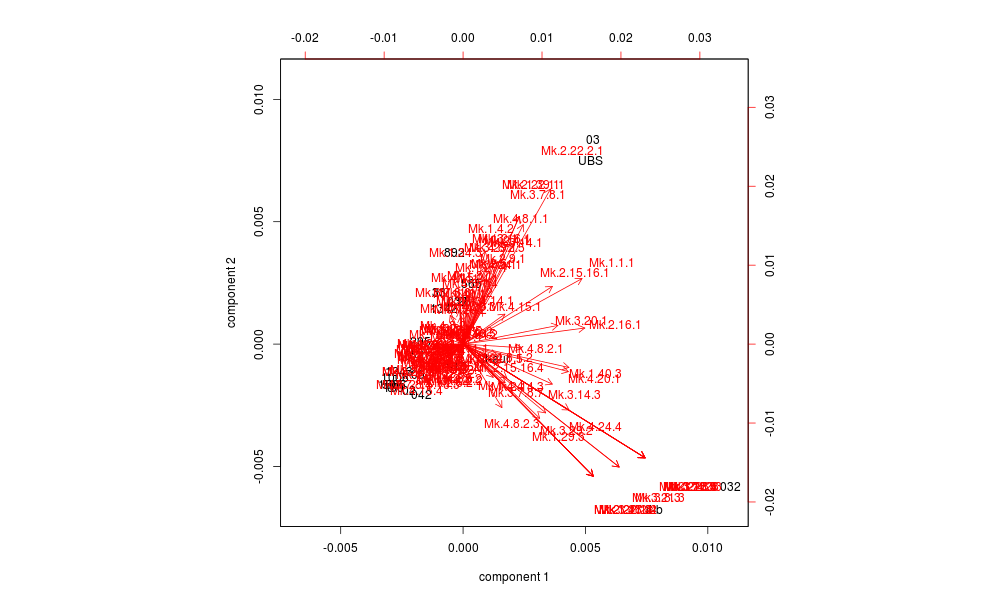
In the DC dendrogram extracted by analysis of the INTF distance matrix, manuscripts 05 and 032 split away first to form solitary branches. The remaining witnesses split three ways at a group to group distance of about 0.35. One group contains a number of manuscripts often styled “Alexandrian.” Another is comprised of 038 and 565, which B. H. Streeter listed as primary authorities of the “Caesarean” text.[9] The third contains a number of known textual complexes including the Byzantine text (011, 07, ..., 1326), von Soden's Iβ (1279, 1528, ..., 752), Family Π (017, 041, ..., 021), Family 1 (1, 1582, ..., 28), Family 13 (124, 13, ..., 983), and Family 1424 (1241, 1424, ..., 954). A number of the dendrogram branches correspond to regions of higher witness density found in the associated CMDS map. The divisive coefficient for this dendrogram is 0.8.
The control data matrix was produced by configuring the generating program to make 151 cases with 503 variables per case while aiming for a mean distance between cases of 0.159. The distance matrix obtained from this data matrix has values ranging from 0.099 to 0.235, less than a third of the distance range found in the primary example. The mean distance between cases hits the mark of 0.159 that the generating program aimed to produce. Analysis of this distance matrix produces a CMDS map with a roughly spherical inner core surrounded by numerous outliers. The proportion of variance for this map is 0.07, much less than the value of 0.32 obtained for the map derived from INTF data. The control DC dendrogram has a divisive coefficient of 0.37, considerably less than the corresponding value of 0.8 obtained for the primary example. The contrast between the INTF data set for Mark's Gospel and the analogous data set comprised of randomly produced cases again points to the existence of grouping among New Testament witnesses.
The CMDS maps obtained for the Gospel of Mark using the UBS4 and INTF data sets have a number of similarities. However, there are conspicuous differences as well. Two of the four regions of higher witness density found in the two maps can be identified with each other. What to call each region presents a problem but conventional labels will do for now. In the UBS4 map, the regions of higher density may be labelled as follows:
-
“Byzantine”
-
“Alexandrian” (e.g. 01, 03, 04, 019)
-
“Western” (e.g. 05, it-a, it-b, it-d)
-
“Family 1” (e.g. f-1, 28, 205).
Regions of the INTF map may be labelled in a similar way:
-
“Byzantine”
-
“Alexandrian” (e.g. 01, 03, 04, 019)
-
“Family 1” (e.g. 1, 205, 209, 1582)
-
“Family 13” (e.g. 13, 69, 346, 543).
The correspondence between the two maps for regions labelled as “Byzantine” and “Alexandrian” is plain enough to require no further comment. As for differences, the INTF map does not have a counterpart for the “Western” group of the UBS4 map but, surprisingly, puts Codex Bezae (05) in the vicinity of Family 1. Also, the UBS4 map does not have a counterpart for the “Family 13” group found in the INTF map. Instead, the entity which represents Family 13 in the UBS4 apparatus (f-13) is located near the “Family 1” group.
There is an explanation for these differences. Each CMDS map reveals groups found in the corresponding data set. The UBS4 data set has only a single entity to represent Family 13 (i.e. f-13) and the INTF data set has only a single representative of the “Western” family of texts (i.e. 05). If the data sets incorporated more witnesses of the respective families then CMDS analysis results would contain corresponding groups. It seems that in the absence of multiple representatives of a group, CMDS analysis can place a solitary case closer to other groups than would occur if more members of its tribe were included. Perhaps the difference in location which would be expressed if more members of a group were included is being pushed into higher dimensions than those presented in a three-dimensional analysis result.
The DC dendrograms derived from the UBS4 and INTF data sets both contain “Alexandrian” (e.g. 01, 03, 04, 019) and “Byzantine” (e.g. 07, 09, 011, 013) branches. There is also consensus concerning the membership of a number of other branches when witnesses present in both data sets are considered. For example, the following branches which appear in the UBS4 dendrogram have counterparts in the INTF dendrogram: 022 and 042; 1241, 1424, and slav; 038 and 565. Apart from inclusion of the Family 13 entity (f-13), the branch of the UBS4 dendrogram comprised of f-1, f-13, 28, and 205 is comparable to the Family 1 branch of the INTF dendrogram (1, 28, ..., 2542).
One difference between the dendrograms relates to 05 and 032, which are solitary in the INTF dendrogram but occupy the same branches as other witnesses in the UBS4 dendrogram. The lack of companions for 05 is consistent with the absence of other “Western” representatives in the INTF data set. The INTF distance matrix confirms that 032 is solitary, being located a relatively large distance from all other witnesses. When witnesses are ranked by distance from 032, the closest (022) belongs to the “Byzantine” complex while the next closest six (2193, 205, 209, 28, 1, 1582) are all members of Family 1. These factors help to explain why 032 is solitary in the INTF dendrogram but shares the same branch as Family 1 in the UBS4 dendrogram. Rather than being contradictory, both dendrograms reveal actual characteristics of 032.
Another difference relates to Family 13, which constitutes a separate branch of the INTF dendrogram. By contrast, the entities which represent Families 1 and 13 in the UBS4 apparatus (i.e. f-1 and f-13) occupy the same branch in the UBS4 dendrogram. The distance between these entities in the UBS4 distance matrix is 0.360; in the INTF distance matrix, minuscules 1 and 13 are a distance of 0.209 apart. By comparison, the mean witness to witness distance is 0.471 for the UBS4 distance matrix and 0.159 for the INTF distance matrix. That is, the distance from f-1 to f-13 is less than the mean distance for the UBS4 data set while the distance from minuscule 1 to minuscule 13 is greater than the mean distance for the INTF data set. This suggests an inconsistency between the two data sets affecting Family 1 or 13 or both. Perhaps one of the entities which represent these families in the UBS4 apparatus does not adequately represent its family? The disparity might also occur if minuscules 1 and 13 were not central members of their respective families.
Yet another difference is that the UBS4 dendrogram puts minuscule 28 in the same branch as the entity which represents Family 13 (f-13) while the INTF dendrogram locates 28 in the Family 1 branch. According to the UBS4 distance matrix, the closest three items to 28 are f-13, 205, and f-1. For the INTF distance matrix, fifteen of the nineteen closest witnesses to 28 are members of Family 1 or 13, with Family 1 members tending to precede those of Family 13. These fifteen include all but one of the members of Families 1 and 13 identified by the relevant branches of the INTF dendrogram, minuscule 983 being the only one left out. Thus, both dendrograms accurately reflect the situation of minuscule 28 relative to Families 1 and 13 implied by the associated distance matrices. The INTF data set, which is more comprehensive with respect to Greek manuscripts, shows that minuscule 28 is more closely related to Family 1 than Family 13.
Comparing these analysis results has been instructive. The cases of Codex Bezae and Family 13 show how sensitive results can be to the mix of witnesses selected for inclusion in a data set. The case of Codex Bezae also shows that an apparent affiliation indicated by one analysis method should be regarded with suspicion if not confirmed by other methods. Recourse to the distance matrix often provides a better understanding of cases for which analysis results are puzzling.
Both the UBS4 and INTF data sets exhibit weaknesses with respect to representing the New Testament textual tradition of Mark's Gospel. The UBS4 data set suffers from a relative lack of variation sites and Greek manuscripts, and there may be a problem with the entities it uses to represent Families 1 and 13. At the same time, the INTF data set lacks early versions and patristic citations which offer a valuable context for understanding affiliations among the Greek manuscripts.
Jerome says in his prologue to the Vulgate version of the Four Gospels,
For if we are to pin our faith to the Latin texts, it is for our opponents to tell us which; for there are almost as many forms of texts as there are copies. If, on the other hand, we are to glean the truth from a comparison of many, why not go back to the original Greek and correct the mistakes introduced by inaccurate translators, and the blundering alterations of confident but ignorant critics, and, further, all that has been inserted or changed by copyists more asleep than awake? ... I therefore promise in this short Preface the four Gospels only, which are to be taken in the following order, Matthew, Mark, Luke, John, as they have been revised by a comparison of the Greek manuscripts. Only early ones have been used.[10]
The UBS4 map for the Gospel of Mark shows that Jerome's revision (vg) lies close to a trajectory which runs between a cluster of Old Latin texts such as Vercellensis (it-a), Veronensis (it-b), Colbertinus (it-c), and Bezae (it-d) at one end and “Byzantine” texts at the other. If these Old Latin texts represent the Latin exemplars used by Jerome, it seems that the “early” Greek manuscripts he used to revise the Latin text of Mark were of the Byzantine variety.
As a first step towards establishing what constitutes a significant distance between two witnesses, one might consider the number of readings per variation unit. The following table due to Gerd Mink is based on figures for the Letter of James fascicle of the INTF's Editio Critica Maior:[11]
Table 6. Distribution of numbers of readings
| Number of readings | Frequency | Cumulative proportion |
|---|---|---|
| 2 | 418 | 0.597 |
| 3 | 124 | 0.774 |
| 4 | 71 | 0.876 |
| 5 | 37 | 0.928 |
| 6 | 25 | 0.964 |
| 7 | 6 | 0.973 |
| 8 | 6 | 0.981 |
| 9 | 6 | 0.990 |
| 10 | 3 | 0.994 |
| > 10 | 4 | 1.000 |
This shows that more than half of the variation sites have only two readings, about three quarters have three or less, and only about one quarter have four or more when many New Testament manuscripts are compared. These numbers are dependent on the editorial policy used to define variation site boundaries and therefore apply only to the data upon which the ECM is based. Nevertheless, they show that there are usually only a few alternatives at each place where the text varies. If this is the case when many manuscripts are compared, it is reasonable to expect that the numbers of alternative readings known to a typical reader or scribe at a variation site would have been even less. Accordingly, when a reader or scribe knew there were alternatives, he or she would usually have known of only two, sometimes three, rarely more.
The manuscript evidence shows that the copying process was inherently conservative. Klaus Wachtel writes,[12]
The ... figures impressively demonstrate the degree of coherence between New Testament manuscripts... This evidence enforces the conclusion that the efforts of scribes to copy their exemplar as precisely as possible were, on the whole, successful. A chain of closely related copies connects the single manuscript texts with the source of the tradition, the initial text.
However, the evidence also shows that scribes and readers regularly marked up manuscripts with alternative readings, deleting a phrase here and adding one there. If a scribe copied a manuscript that included such markup, a decision concerning how to deal with alternatives was required at every place where they occurred. (Nothing has changed!) When faced with such a choice, the scribe might choose one of the options or combine more than one to produce a conflation.
This is not the only way that alternative readings entered the text. A reader or copyist could also create a novel reading without any manuscript authority, perhaps in an attempt to repair an apparent corruption or to "improve" the text where there was a perceived difficulty. Then there were unconscious alterations: involuntary additions, substitutions, and omissions which occurred in the process of a copyist reading the exemplar, remembering its words, then writing them down in the copy. These actions sometimes created nonsense readings which would subsequently attract the attention of a reader or copyist seeking to repair faults in the copy.
Considering the variations alone, a copying event can be modelled as a sequence of choices between readings at a series of variation sites. Not every reading at a variation site would have had the same chance of being selected in a particular copying event. One reading might have stood out as preferable for doctrinal, stylistic, or parochial reasons. Then again, none might have been favoured. It is impossible to say with confidence which alternative was more likely to be chosen by a copyist, although there does seem to have been a preference for readings found in near relatives of the manuscript at hand. As Gerd Mink writes, “In a dense tradition, it is typical of contamination that a witness shares most of its variants with its closest relative and if it deviates from this relative the variants concerned can be found in other close relatives.”[13]
While there is no way to determine the probability that a given reading would have been chosen by a copyist working at a particular place and time, it is possible to make an estimate based on the relative frequency of the reading among extant witnesses. A refinement would be to consider the relative frequency of a reading among closely related witnesses. Yet another approach would be to assume equal probabilities among readings which are relatively common, excluding rarities altogether.
Adopting the last approach and assuming the common case of only two possible readings per variation unit results in a particularly simple model where each copying event is represented by a sequence of trials, each trial comprised of selecting one alternative from two equally probable states. The model applies to a copyist selecting a series of readings from an exemplar whose variation sites each have only two readings with apparently equal merit. From a statistical perspective, the model is equivalent to a series of coin tosses using an unbiased coin. This equivalence allows a minimum standard to be established for what constitutes a statistically significant level of disagreement between two witnesses.
If there are two equally probable states (i.e. readings) for each trial (i.e. selection
of a reading at a variation site), the chance of disagreement at each place where a
choice has to be made is one half. This is because there are four possible combinations
of two states chosen in two trials, half of which constitute disagreement. To
illustrate, if the two states are represented by the numerals 1 and 2 then the four possible combinations are
(1, 1), (1, 2), (2, 1), and (2, 2), the second and third of which disagree.
The binomial distribution applies to the outcomes of multiple independent trials when the outcome of each trial can have only two states and the respective probabilities of the two states are the same for each trial. By convention, the two states are labelled success and failure. Given a particular number of trials and a fixed probability of success, the binomial distribution describes how frequently each number of successes occurs. Using this distribution, it is possible to obtain critical limits, which are the upper and lower bounds of a confidence interval that specifies the range of numbers of successes that can be confidently attributed to chance. Before obtaining the limits, it is necessary to select an alpha value, which represents an acceptable level of error. While any number of successes between zero and the number of trials can occur, only a central range of numbers of successes is likely. Over many repeats of an experiment consisting of a set number of trials, numbers of successes outside this central range will occur with a relative frequency equal to the alpha value. If the alpha value is small enough then it is reasonable to assert that a number of successes outside the range defined by the confidence interval is not due to chance. However, such an assertion is expected to be wrong in the proportion of cases corresponding to the alpha value. For this article, an alpha value of 5% is used, producing a 95% confidence interval. Given this alpha value, one expects to be wrong only 5% of the time when asserting that a value outside the 95% confidence interval is not due to chance.[14]
Dividing a number of successes by the total number of trials produces a proportion of success. The following table presents 95% confidence intervals for proportions of success expected to occur by chance for various numbers of trials where each trial has a probability of success equal to one half. Each interval uses the notation [lower, upper], where lower and upper are the inclusive limits of the range. The intervals given in the table relate to the simple model where each trial consists of two random selections from two equally probable states. As a success corresponds to a disagreement between two randomly selected states, the proportion of successes corresponds to the proportion of disagreements, which is the simple matching distance.[15]
Table 7. 95% confidence intervals (p = 0.5)
| No. of trials | Interval |
|---|---|
| 5 | [0.000, 1.000] |
| 10 | [0.200, 0.800] |
| 15 | [0.267, 0.733] |
| 20 | [0.300, 0.700] |
| 50 | [0.360, 0.640] |
| 100 | [0.400, 0.600] |
| 200 | [0.430, 0.570] |
| 500 | [0.456, 0.544] |
| 1000 | [0.469, 0.531] |
| 2000 | [0.478, 0.522] |
These intervals only apply to the special case of each variation unit having two equally probable readings. Nevertheless, the table illustrates some important points:
-
Calculating a distance from too few variation units is a futile exercise because any distance thus obtained is reasonably attributable to chance. In this case, if five or less variation units are being compared then no distance is outside the range expected to occur when states are randomly selected.
-
The relative size of the confidence interval bounded by the upper and lower critical limits decreases with the number of trials. Here, the relative size of the interval is 100% for five, just under 50% for fifteen, and 20% for one hundred trials.
-
Just as a distance less than the lower bound of a confidence interval is statistically significant, so is one greater than the upper bound. To use the example of one hundred trials given in this table, a distance between two witnesses which is larger than 0.6 is just as unexpected as one less than 0.4.
The simple model is based on a number of assumptions which do not apply to data derived from large-scale collations. For example, a typical scribe would only have known about a fraction of the variations which manifest when a large number of copies are compared. Also, a typical scribe did not have an equal preference for alternatives at every variation site. Furthermore, editorial definition of variation site boundaries affects the distribution of the number of alternative textual states per variation unit. A more realistic approach establishes critical limits by reference to the distribution of witness to witness distances found in the data set being studied.
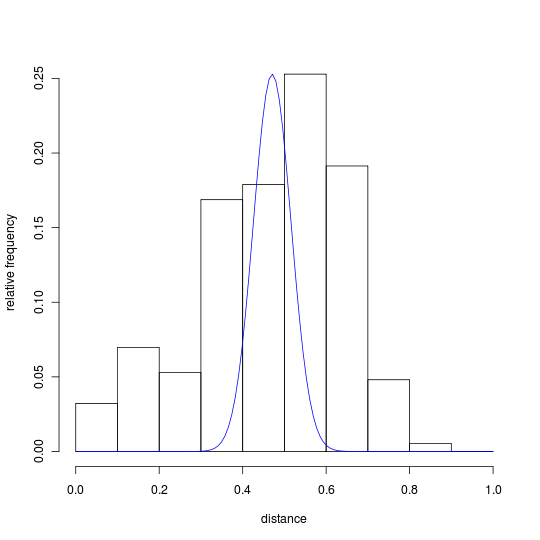
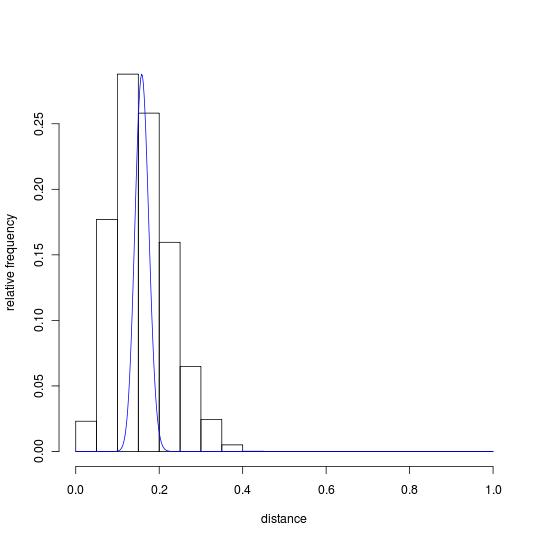
The following histograms show distributions of simple matching distances for the UBS4 and INTF data sets for Mark:
A blue binomial curve is superimposed on each histogram to show the range of distances expected to occur for unrelated pairs of witnesses. These curves were generated by an R expression which uses the following parameters to obtain relative frequencies from the binomial distribution:[16]
-
the number of trials as estimated by the rounded mean number of variation units from which entries in the distance matrix were calculated
-
the probability of success as estimated by the mean value of distances in the distance matrix.
A binomial curve generated from mean values for the number of variation units and distance between witnesses shows the typical range of distances which is expected to occur by chance. However, there are reasons why such a range should not be expected to apply to all pairs of witnesses in the data set. First, the readings of a witness might not be well defined at every variation unit so the number of variation units used to calculate a distance can vary from one pair of witnesses to the next. Second, the expected distance between witnesses may vary. Fortunately, the curves are not particularly sensitive to changes in these parameters. Nevertheless, if the values for the entire data set are far different to those appropriate for a particular set of witnesses then it is better to use the particular values to obtain the corresponding expected range of distances. To illustrate, if one were interested in a fragmentary witness then the number of trials would be constrained by the number of variation units at which its readings are defined. As another example, if one were studying a closely related subset of witnesses then the probability of success would be the mean distance between members of that subset.
The following table gives the 95% confidence intervals obtained for the UBS4 and INTF data sets by using this approach. The critical limits correspond to an alpha value of 5%, a number of trials equal to the mean number of variation units, and a probability of success equal to the mean distance between pairs of witnesses:[17]
Table 8. 95% confidence intervals for distance
| Data set | Mean no. of variation units | Mean distance | Interval |
|---|---|---|---|
| UBS4 (Mark) | 123 | 0.471 | [0.382, 0.561] |
| INTF (Mark) | 488 | 0.159 | [0.127, 0.193] |
Any distance between the upper and lower limits of an interval is normal in the sense of not being unexpected if readings are randomly chosen. A distance outside this range is not expected to happen by chance: if less than the lower limit then the relevant pair of witnesses are adjacent, being closer together than normal; if greater than the upper limit there is an opposite relationship, the pair being further apart than normal. An active process is implied for distances outside the normal range, one which has either driven texts closer together or further apart than would be expected if readings had been chosen at random. For the UBS4 data set, the lower limit is 0.382, corresponding to a percentage agreement of 61.8%. Thus, for this data set, a percentage agreement greater than 61.8% is significant in a statistical sense. For the INTF data set, a distance less than 0.127, corresponding to a percentage agreement greater than 87.3%, is statistically significant.
We are now in a position to provide another answer to the question posed earlier: “At what height should a dendrogram be cut to
produce groups where members are actually related?” A reasonable value
to use for this purpose is the lower bound of the range of distances which are likely to
occur by chance for a given data set. To illustrate, the control for the well defined
groups example is comprised of twelve cases with fifteen variables per case and a mean
distance between cases of 0.481. The corresponding lower critical limit is 0.267.[18] Cutting the relevant dendrogram at this height succeeds in
assigning most cases to solitary groups, as is appropriate because the cases are
unrelated. However, cutting at that height also produces two spurious groups as well,
one containing R4 and R8, the other
R5 and R11. This serves as a
reminder that pairs of randomly generated cases can occasionally be closer together or
further apart than expected. In the long run average of many trials, the frequency of
such cases approaches the alpha value.
The upper critical limit is also useful in the context of dendrograms. Branches obtained by cutting a dendrogram at the upper limit represent super-structures which are more dissimilar than would be expected if their members were comprised of randomly chosen states. Using the UBS4 dendrogram as an example, cutting at the upper critical limit (0.561) produces this partition:
Table 9. UBS4 witnesses partitioned by cutting at the upper critical limit
| Cluster | Members |
|---|---|
| 1 | UBS 01 03 04 019 037 044 892 2427 cop-sa cop-bo |
| 2 | 02 33 157 180 579 597 700 1006 1010 1071 1241 1243 1292 1342 1424 1505 Byz 07 09 011 013 022 042 Lect syr-p syr-h |
| 3 | 05 038 565 it-a it-aur it-b it-c it-d it-f it-ff-2 it-i it-l it-q it-r-1 vg Augustine |
| 4 | 032 |
| 5 | f-1 f-13 28 205 |
| 6 | it-k |
| 7 | syr-pal |
| 8 | syr-s arm geo |
The sampling error of a distance between two texts is the difference between the actual distance that would be obtained by examining the entire population of variation sites and the estimated distance obtained from a sample of the places where the two texts vary. The actual distance is a parameter obtained from the entire population of variations while the estimated distance is a statistic obtained from a sample. In practice, almost every text to text distance is a mere estimate because of two common circumstances which prevent the entire population of variations being examined:
-
witnesses are compared by reference to a critical apparatus which does not list every variation
-
one or both of the witnesses being compared may be fragmentary.
In the first case, only a sample of variation units is used for the comparison. In the second, a smaller number of variation units is compared than would be the case if both witnesses were complete.
The actual distance can only be determined by examining the entire population of variations. Nevertheless, a distance estimated from a sample is still useful provided that one knows how well it is expected to approximate the actual value. This piece of information is supplied by a statistical analysis of the sample to produce a confidence interval which probably contains the actual distance. The interval's limits are calculated from the binomial distribution using the estimated distance as the probability of success and the number of compared variation units as the number of trials. To illustrate, the following table gives a distance estimate and 95% confidence interval obtained when variables are randomly selected from two of the cases found in one of the example data sets:[19]
Table 10. Estimated distances and their confidence intervals (alpha value = 0.05)
| Data set | Cases compared | Places compared | Distance estimate | Confidence interval |
|---|---|---|---|---|
| Well defined groups | A1 A12 | 5 | 0.600 | [0.200, 1.000] |
| Well defined groups | A1 A12 | 15 | 0.533 | [0.267, 0.800] |
| UBS4, Mark | f-1 f-13 | 5 | 0.600 | [0.200, 1.000] |
| UBS4, Mark | f-1 f-13 | 50 | 0.380 | [0.240, 0.520] |
| UBS4, Mark | f-1 f-13 | 100 | 0.340 | [0.250, 0.430] |
| INTF, Mark | 1 13 | 5 | 0.400 | [0.000, 0.800] |
| INTF, Mark | 1 13 | 50 | 0.220 | [0.120, 0.340] |
| INTF, Mark | 1 13 | 100 | 0.200 | [0.120, 0.280] |
| INTF, Mark | 1 13 | 400 | 0.217 | [0.177, 0.258] |
Another way to express a confidence interval is by giving an estimated value and a margin of error. The lower margin of error is the difference between the lower critical limit and the estimate while the upper margin of error is the difference between the estimate and upper critical limit. If the interval is symmetrical with respect to the estimate then the upper and lower margins are the same and the expression estimate ± margin can be used to specify the estimate and its confidence interval.[20]
As can be seen from the table, estimates based on only a few places of comparison are unreliable because the range of values expected to occur for an estimate (i.e. the confidence interval) covers a large part of the range of possible values. Increasing the number of places compared makes the relative size of the confidence interval decrease. It is therefore desirable to use as many variation units as possible when estimating distances between witnesses. However, one is sometimes forced to use a lesser number, as when fragmentary witnesses are involved. What then is an acceptable lower limit for the number of variation units? There is no absolute guide so every researcher has to decide what is appropriate. In this article, a distance is only used if calculated from a minimum of fifteen variation units where both witnesses are defined. In order to satisfy this standard, the program which calculates a distance matrix first goes through an iterative process, dropping the least well defined member of the least well defined pair at every step until all remaining distances are calculated from at least the minimum acceptable number of variation units.
Given a distance matrix, it is straightforward to rank witnesses by distance from a reference witness. Furthermore, if the number of defined variation units is counted for each witness then a confidence interval can be established for each distance estimate. It is then possible to identify adjacent and opposite witnesses with respect to a reference witness. Those which are adjacent are less distant than the lower limit of the relevant interval while those which are opposite are more distant than the upper limit. To illustrate, the following table ranks witnesses by distance from the entity which represents Family 1 in the UBS4 data set (i.e. f-1). Any distance which is not statistically significant is marked by an asterisk.[21]
Table 11. Ranked distances from f-1 (UBS4, Mark)
| 205 (0.044); 28 (0.338); Lect (0.339); f-13 (0.360); 1424 (0.366); 1241 (0.370); geo (0.372); 1505 (0.378); slav (0.379); G (0.389*); 1243 (0.390*); Byz (0.391*); 1292 (0.392*); 1006 (0.412*); 1071 (0.412*); 597 (0.418*); 180 (0.419*); E (0.419*); 1010 (0.421*); 565 (0.425*); A (0.426*); H (0.426*); 33 (0.427*); syr-h (0.430*); syr-p (0.431*); arm (0.432*); 700 (0.434*); F (0.435*); Sigma (0.437*); syr-s (0.438*); 157 (0.450*); Theta (0.455*); 579 (0.455*); it-q (0.456*); syr-pal (0.458*); vg (0.465*); 1342 (0.474*); Augustine (0.479*); it-l (0.481*); N (0.484*); it-aur (0.492*); it-f (0.505*); 892 (0.511*); C (0.514*); eth (0.517*); W (0.537*); L (0.539*); cop-sa (0.560*); Psi (0.567*); it-i (0.568*); Delta (0.570); cop-bo (0.579); it-ff-2 (0.589); it-b (0.593); it-c (0.595); it-r-1 (0.611); 2427 (0.615); it-a (0.635); UBS (0.642); Aleph (0.656); B (0.672); D (0.679); it-k (0.683); it-d (0.690) |
This shows that f-1 is adjacent to 205, 28, Lect, f-13, 1424, 1241, geo, 1505, and slav. Many witnesses (G ... it-i) occupy the middle ground with distances from f-1 which are not statistically significant. There may be a relationship with f-1 in each case but the sampling error associated with the available number of defined variation units in the data set is too large to allow a confident decision to be made on the matter. At the other end of the scale, f-1 is opposite to Delta, cop-bo, it-ff-2, it-b, it-c, it-r-1, 2427, it-a, Aleph, B, D, it-k, and it-d. This indicates that Family 1 is non-Western and non-Alexandrian in the Gospel of Mark.[22]
The random walk is a class of problem which considers how far from the starting point a thing will end up if every movement is random. The classic example is a drunk staggering along a gutter. The man is so drunk that a forward or backward step is equally likely. How far from the beginning will the drunk end up? If this scenario is extended into two dimensions then the drunk could end up anywhere on a flat surface within a maximum distance of his beginning point, that maximum being the number of steps times the average step length. For three dimensions, the final location would be anywhere within a sphere of the same maximum radius. While possible for the drunk to take a step in the same direction every time, it is unlikely. In fact, the drunk will probably end up somewhere within a smaller distance of the origin, which distance is the order of the square root of the number of steps times the average step length.
To the extent that the New Testament textual tradition can be modelled as random choices among readings, one might expect the diameter of the point cloud in a CMDS diagram to be about the same as obtained for a random data set of the kind generated for the controls presented above. As it happens, the diameters of a number of the major clusters in the CMDS maps of the UBS4 and INTF data sets are approximately the same as the diameters of the relevant control maps, which are about 0.3 and 0.1, respectively.[23] However, the distances between the outermost witnesses in the CMDS maps of the UBS4 and INTF data sets are greater than the relevant control CMDS map diameters, implying that these witnesses are further apart than expected if random processes alone were to blame for the differences.
What might explain these larger than expected differences? One possibility is conscious selection among readings which resulted in distinctive texts, perhaps due to theological differences between the users (or promulgators) of those texts. Another possibility is suggested by the apparent association of certain clusters with early versions:
Table 12. Association of clusters and early versions
| Cluster | Early version |
|---|---|
| Alexandrian | Coptic (e.g. cop-bo, cop-sa) |
| Western | Old Latin (e.g. it-a, it-b, it-c, it-d) |
| Family 1 | Old Syriac, Armenian, Georgian (syr-s, arm, geo) |
Perhaps the early versions were players in the New Testament's divergence into some of the major textual streams seen in the analysis results? It is not unreasonable to expect that a scribe copying a Greek manuscript in a region where a particular version prevailed would tend to make the Greek conform to a back-translation of that version.
Analysis techniques such as classical multidimensional scaling and divisive clustering reveal how many groups exist when the groups are well defined. However, these techniques do not give clear guidance on the number of groups when grouping is poorly defined. As shown above, a classical multidimensional scaling map produced from randomly generated cases exhibits density fluctuations which might be mistaken for actual groups; also, divisive clustering can be used to partition a data set which does not contain any groups.[24]
The problem of how to define a group is exacerbated by the phenomenon of mixture. Viral readings have leapt from text to text, making it harder to untangle the strands of textual transmission. Mixture blurs the boundaries of textual groups, causing each to merge into its neighbours. In the case of the New Testament text, mixture is so ubiquitous and the number of copies so large that one cannot expect there to be vacant regions between groups. A chain of closely related witnesses can usually be found to connect even the most disparate ones. There is no reason to expect large gaps between families of witnesses. If such a gap does exist then it is quite possibly due to an accident of history whereby witnesses that once occupied the space are now lost.
Fortunately, there are modes of multivariate analysis which allow groups to be discovered even when mixture is present. One such technique called partitioning around medoids (PAM) divides the cases of a data set into a predetermined number of groups. A set of this many representative cases called medoids is then chosen so that the sum of all distances from cases to the selected medoids is a minimum. This technique is more robust than another popular partitioning technique called k-means clustering because it is less sensitive to noise (e.g. sampling error) and outliers (e.g. eccentric cases). There are two phases to the procedure:[25]
-
build: the algorithm selects a tentative set of medoids
-
swap: cases are swapped with tentative medoids until no further reduction in the sum of distances occurs.
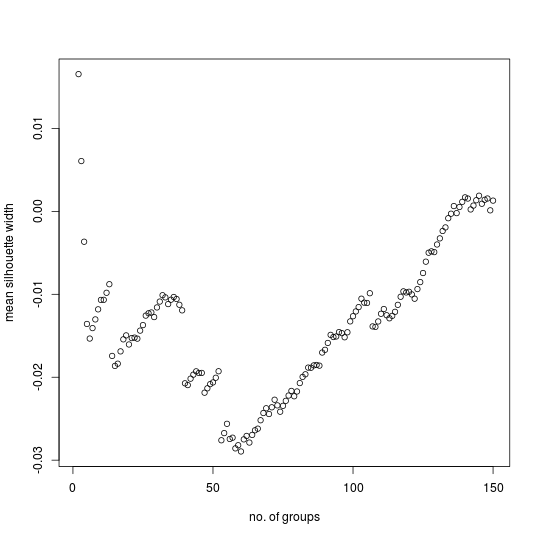
It may seem preposterous to use a grouping technique which requires the number of groups to be specified beforehand. After all, the aim is to discover groups, not to make arbitrary decisions about how many there might be. Fortunately, a statistic called the silhouette width provides a way forward. A silhouette width approaching a value of one indicates that a case is in the correct cluster, a value approaching zero indicates that a case lies between clusters, and a negative value indicates that a case is probably placed in the wrong cluster. The mean silhouette width (MSW) is the average of all silhouette widths obtained when a particular number of groups is specified. The MSW tends to be greater when the preordained number matches how many groups are actually contained in the data. Consequently, peaks in a graph of MSW versus numbers of groups indicate how many groups actually exist. The MSW tends to decrease as the number of groups increases so it is worth considering more than just the first peak when trying to discern preferable numbers of groups for a data set.
The use of PAM analysis in conjunction with the mean silhouette width to discover how many groups exist will now be demonstrated by reference to the example data sets.
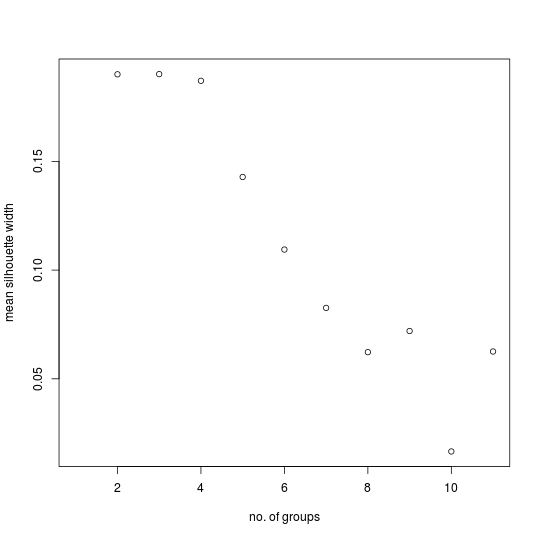
Plotting the MSW versus number of groups for the first example produces this result:
The MSW value is given for each number of groups from two up to one less than the number of cases in the data set. The tendency for the MSW to decrease as the number of groups increases is apparent. Local maxima occur for three, seven, eleven, and seventeen groups. Using PAM to partition the data set into three groups produces the following divisions:
Table 13. PAM division of cities into three groups
| Medoid | Members |
|---|---|
| DFW | ATL ORD LAX DFW DEN JFK PHX LAS IAH CLT MCO MIA SFO |
| HKG | PEK HND BKK HKG CGK SIN CAN PVG KUL SYD |
| FRA | LHR CDG FRA DXB MAD AMS MUC |
Comparing with the corresponding CMDS map shows that this partition makes sense with respect to the geographical distribution of the cities, having isolated North American, Asian, and European groups. A similar partition is obtained by cutting the corresponding DC dendrogram at a height of 6,000 km although DXB (Dubai) and SYD (Sydney) form solitary branches when that is done. The medoids identified by PAM analysis are DFW (Dallas and Fort Worth), HKG (Hong Kong), and FRA (Frankfurt). These stand near the geographical centres of the regions associated with the groups.
The next local maximum occurs for seven groups. The corresponding partition also makes sense when compared with the geographical data:
Table 14. PAM division of cities into seven groups
| Medoid | Members |
|---|---|
| ATL | ATL ORD DFW JFK IAH CLT MCO MIA |
| PVG | PEK HND HKG CAN PVG |
| CDG | LHR CDG FRA MAD AMS MUC |
| LAS | LAX DEN PHX LAS SFO |
| SIN | BKK CGK SIN KUL |
| DXB | DXB |
| SYD | SYD |
The North American group is now split east-west, the Asian group is split north-south, and the two most isolated cases (DXB and SYD) form singletons. (A singleton is a set that contains only one element.)
While the exercise could be continued with the other numbers of groups identified by the MSW plot, these two partitions suffice to show the merit of the approach. The example of distances between cities shows that sensible groupings are obtained even though there is no “correct” number of groups for the data set.
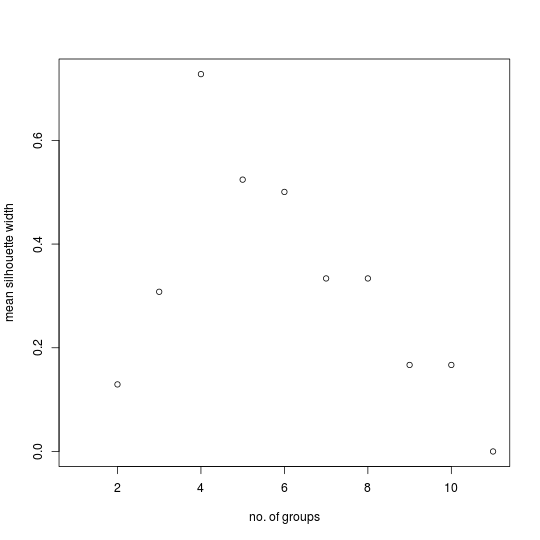
The primary example of the data set for well defined groups does have a “correct” number of groups, which is four. Here are the MSW plots for this primary example and its control:
At first glance these two do not seem very different. Both exhibit a tendency for the mean silhouette width to decrease as the number of groups increases. However, there is a major difference. The highest peak for the primary example (0.728) is more than three times greater than the highest peak of the control (0.190). Given that the control is based on randomly generated cases, it is prudent to ignore any peak in the primary example if its magnitude is not much greater than the value obtained for the same number of groups in the control.
The highest peak in the primary example's MSW plot correctly identifies the number of groups in the data set. The corresponding partition correctly assigns the cases to their respective groups:
Table 15. PAM division for well defined groups
| Medoid | Members |
|---|---|
| A3 | A1 A2 A3 |
| A4 | A4 A5 A6 |
| A8 | A7 A8 A9 |
| A12 | A10 A11 A12 |
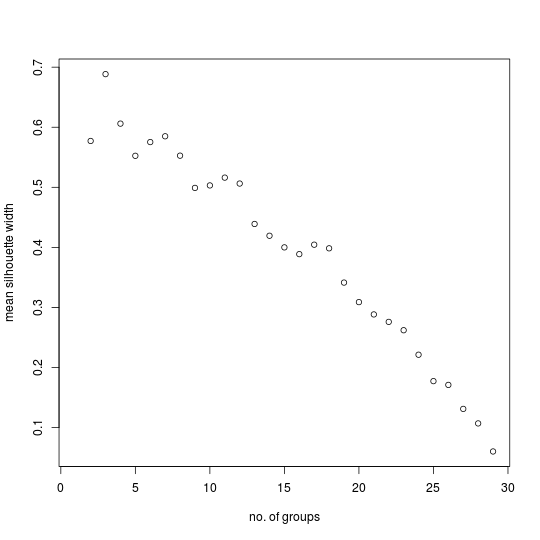
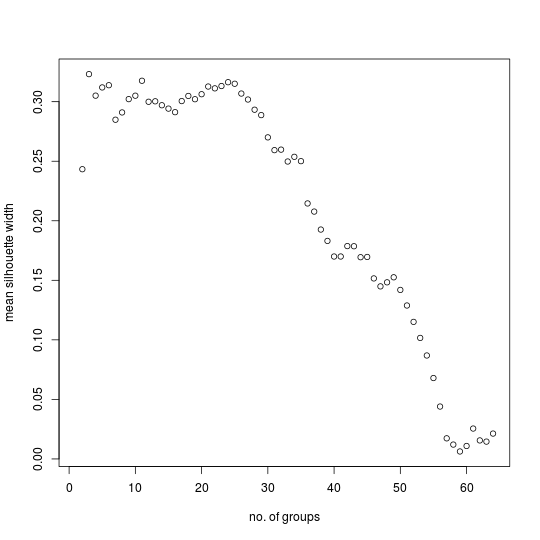
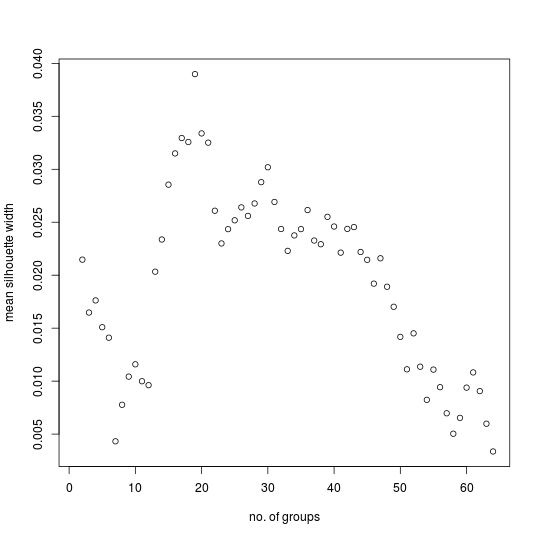
Comparing MSW plots for the primary example and control of the UBS4 data set for the Gospel of Mark shows that peaks in the first plot are well above the noise level indicated by the second plot until the number of groups reaches about sixty.
The first plot has quite prominent peaks that exceed the noise level for three, six, eleven, twenty-four, thirty-four, forty-two or forty-three, and forty-nine groups. As far as grouping is concerned, this data set is like the example for inter-city distances rather than the one for well defined groups in as much as there is no clear winner, no “correct” number of groups. Instead, certain numbers of groups have greater claim than others to be “natural” when partitioning the data set. For such a data set, peaks in the MSW plot are suggestive rather than emphatic.
One is then left wondering what number of groups is best. In this case, the peak at twenty-four groups seems particularly conspicuous in view of the general tendency for the mean silhouette width to decrease as the number of groups increases. However, dividing the witnesses into so many groups tends to dissolve larger entities which, though not as coherent as ones which remain together, are nevertheless important for comprehending the broad structure of the textual tradition. Partitions of the UBS4 data set based on three, six, eleven, and twenty-four groups will therefore be presented below.
Using PAM analysis to split the UBS4 data set into three groups produces these divisions:
Table 16. PAM result (UBS4, three groups)
| Medoid | Members |
|---|---|
| 044 | UBS 01 03 04 019 032 037 044 892 2427 it-k syr-s cop-sa cop-bo |
| Byz | 02 f-1 f-13 28 33 157 180 205 579 597 700 1006 1010 1071 1241 1243 1292 1342 1424 1505 Byz 07 09 011 013 022 042 Lect it-aur it-f it-l syr-p syr-h syr-pal eth geo slav Augustine |
| it-i | 05 038 565 it-a it-b it-c it-d it-ff-2 it-i it-q it-r-1 vg arm |
| Poorly classified (worst last): 04 syr-s arm vg | |
Being the most central witness makes the medoid a useful representative of its group. In addition, the siglum of the medoid serves as a label. There are reasons why it is better to use a medoid siglum rather than a conventional name such as “Alexandrian,” “Byzantine,” “Caesarean,” “Western,” “Family 1,” or “Family 13” to label a group. For one thing, partitioning a data set into a large number of groups tends to split any structure for which a broad categorical label such as “Alexandrian” might be apt. For another, the most central witness of a textual family is often not the one which the family is named after. Sometimes, however, corresponding groups in different partitions do not have the same medoids. For example, the group with medoid 044 in the three-way partition of the UBS4 data set has the same core members as the one with medoid 03 in a six-way partition of the same data set. A group's medoid can change if even a single case is added or removed because another case can then become the most central one. Consequently, while the medoid does serve as a convenient and appropriate label for a group, it is not a reliable guide to identifying corresponding groups in different partitions of the same data set. A better approach for this purpose is to look for common constituents. If the medoid of a textual complex does change from one partition to the next then the sequence of medoids that complex has for different numbers of groups can be chained together to form a label.
Note
From this point forwards, the medoid siglum will be used to label its group. If groups which have the same medoid but are from different partitions need to be distinguished then the number of groups in the relevant partition will be added to the label in parentheses. If the medoid of a group changes for different partitions of the same data set then the sequence of medoids will be chained together to form a label. E.g. Gr 044 refers to a group whose medoid is 044, Gr Byz (3) to the group with medoid Byz in a three-way partition, Gr Byz (6) to the one with medoid Byz in a six-way partition, and Gr 044/03 to the group whose medoid changes from 044 to 03 in different partitions of the same data set.[26]
The groups which emerge from a three-way partition of the UBS4 data set are in some respects similar to traditional categories: Gr 044 contains a number of “Alexandrian” witnesses, Gr Byz is mainly comprised of “Byzantine” ones, and Gr it-i includes a number of “Western” texts. However, the groups also contain witnesses which are not normally associated with the conventional categories. Some of the witnesses which seem out of place are out of place. In a situation analogous to hammering square pegs into round holes, they do not fit their assigned places. When deciding how to partition a data set, numbers of groups with larger values of the mean silhouette width are preferable. Although the average value of the silhouette widths may be relatively large, individual silhouette widths might be small. Indeed, a case can have a negative value for the statistic, indicating a particularly poor fit to its assigned division. The more negative the silhouette width, the worse the classification. When the UBS4 data set is divided into three groups, witnesses 04, syr-s, arm, and vg are thus identified as not well classified. Nevertheless, assigning them to the indicated divisions still minimizes the sum of distances between medoids and witnesses for the given number of groups.
Dividing the witnesses into six groups gives poorly fitting witnesses the freedom to migrate into new groups where they are more at home. Other witnesses stay in the remnants of groups from the three-way partition.
Table 17. PAM result (UBS4, six groups)
| Medoid | Members |
|---|---|
| 03 | UBS 01 03 019 037 044 2427 cop-sa cop-bo |
| Byz | 02 04 f-13 33 157 180 579 597 700 892 1006 1010 1071 1241 1243 1292 1342 1424 1505 Byz 07 09 011 013 022 042 Lect syr-p syr-h slav |
| it-ff-2 | 05 it-a it-b it-c it-d it-ff-2 it-i it-k it-r-1 |
| arm | 032 565 syr-s arm geo |
| vg | 038 it-aur it-f it-l it-q vg syr-pal eth Augustine |
| 205 | f-1 28 205 |
| Poorly classified (worst last): 038 f-13 geo eth 565 892 | |
In this partition, Gr 03, Gr Byz, and Gr it-ff-2 are reminiscent of traditional “Alexandrian,” “Byzantine,” and “Western” categories. Gr vg is centred on the entity that UBS4 uses to represent the Latin Vulgate. While one might expect Augustine's quotations and a number of Latin manuscripts to be here, it is surprising to find 038, the Ethiopic (eth), and the Palestinian Syriac (syr-pal) included as well. Two of these, 038 and the Ethiopic, have negative silhouette widths to indicate that they are not a good fit. Nevertheless, this partition suggests that 038, the Ethiopic, and the Palestinian Syriac (actually Aramaic) share something in common with the Latin Vulgate and other members of this group. The UBS4 editors date the Ethiopic and Palestinian Syriac versions after the Latin Vulgate. It is thus conceivable that these two versions incorporate passages which amount to translations of the Latin Vulgate.[27]
As for 038, also known as Θ or Codex Koridethi, a glance at the corresponding CMDS map shows that it does seem drawn towards the region of textual space associated with the Latin Vulgate. Using the UBS4 distance matrix to rank witnesses by distance from 038 confirms that a number of its closest neighbours are of the Latin Vulgate kind (e.g. Augustine, vg, it-l):
Table 18. Ranked distances from 038 (UBS4, Mark)
| 565 (0.269); syr-pal (0.373); f-13 (0.390); 700 (0.397); it-i (0.400); Augustine (0.423); slav (0.427); vg (0.429); 28 (0.441); it-l (0.445); 205 (0.449); arm (0.453); f-1 (0.455); it-aur (0.462); geo (0.462); 1424 (0.463); Lect (0.471); it-q (0.472); it-ff-2 (0.476); it-b (0.477); 1071 (0.478); 011 (0.481); 1241 (0.489); syr-h (0.491); 1505 (0.496); 05 (0.500); 1243 (0.500); 1292 (0.500); it-d (0.500); it-r-1 (0.500); syr-p (0.504); eth (0.504); 180 (0.507); Byz (0.508); it-f (0.509); 33 (0.514); 013 (0.516); 597 (0.522); 1006 (0.522); 157 (0.527); 07 (0.529); it-a (0.532); 022 (0.541); it-c (0.542); 042 (0.549); 1010 (0.556); cop-bo (0.558); 02 (0.559); 09 (0.559); 892 (0.563); syr-s (0.565); 579 (0.567); 1342 (0.578); 019 (0.602); 032 (0.612); UBS (0.626); 04 (0.632); cop-sa (0.650); 037 (0.659); 2427 (0.662); 01 (0.664); 044 (0.705); it-k (0.707); 03 (0.725) |
Returning to the six-way partition, all eight members of Gr arm and Gr 205 fall into a category which Streeter regarded as an “Eastern type” having sub-varieties associated with the provincial capitals of Syria and Palestine:[28]
Table 19. Streeter's Eastern type of Gospel text
| Provincial Capitals | ||
|---|---|---|
| Antioch (Syria) | Caesarea (Palestine) | |
| Authorities | ||
| Primary | Sinaitic Syriac | 038, 565 |
| Secondary | Curetonian Syriac | 032 (Mark chapters 6-16), Family 1, Family 13, 28, 700, Georgian |
| Tertiary | Syriac Peshitta, Armenian | 022, 023, 042, 043, 157, 544, Family 1424 |
| Supplementary | Harclean Syriac, Palestinian Syriac | 030, 039, 1071, 1604, Armenian |
Larry Hurtado challenges the view that 032, also known as Codex W or Washingtonensis, has a “Caesarean” text:
If Codex Θ is a good representative of the “Caesarean text,” the poor and unexceptional agreement of Codex W with Θ makes it highly unlikely that W is related in any special way to this text-type.[29]
The textual nature of 032 is thought to change part of the way through the Gospel of Mark, which change Hurtado locates in the vicinity of Mark 5.6. Streeter regarded the latter part of 032 as “Caesarean.” Ranking witnesses by distance from 032 in Mark chapters 6-16 helps to reveal the manuscript's character in this block:[30]
Table 20. Ranked distances from 032 (UBS4, Mark chapters 6-16)
| syr-s (0.421*); arm (0.429*); geo (0.429*); 205 (0.469*); f-1 (0.479*); 565 (0.500*); 28 (0.510*); cop-sa (0.514*); f-13 (0.541*); 044 (0.548*); 038 (0.558); 700 (0.561); it-f (0.569*); vg (0.571); 011 (0.573); it-r-1 (0.574*); cop-bo (0.575); it-l (0.576); syr-p (0.581); Augustine (0.583*); slav (0.587); it-ff-2 (0.589); UBS (0.591); it-q (0.591); 1006 (0.592); 1243 (0.592); it-b (0.595); syr-h (0.598); it-c (0.600); Lect (0.602); 037 (0.608); 1424 (0.608); 180 (0.612); 1071 (0.612); 03 (0.613); 2427 (0.613); eth (0.616); 05 (0.617); 892 (0.619); it-aur (0.621); 02 (0.622); 157 (0.622); 1241 (0.622); 1292 (0.622); Byz (0.624); 597 (0.625); 1010 (0.625); 019 (0.626); it-k (0.627); 01 (0.630); 07 (0.633); it-d (0.633); 04 (0.635); 022 (0.639); 09 (0.640); 013 (0.642); it-i (0.643); 1342 (0.649); 1505 (0.649); 042 (0.651); 579 (0.653); syr-pal (0.667); it-a (0.671); 33 (0.677) |
Hurtado is right to say that agreement between 032 and 038 is poor. In fact, the texts of 032 and 038 have an opposite relationship, being further apart than would be expected to happen by chance. Even so, all of the seven closest witnesses to 032 belong to Streeter's “Eastern” branch although none is adjacent to 032 in the sense of being closer than expected by chance. However, as mentioned before, lack of statistical significance for a distance does not imply lack of relationship between two witnesses. Instead, an adjacent or opposite relationship may exist but it is not possible to confidently say so without analysis of a more comprehensive data set. In the context of the UBS4 data set for Mark, 032 does not have any close neighbours and might therefore be described as an eccentric text. Nevertheless, it remains true that the closest witnesses to 032 in this data set are members of Streeter's “Eastern” category.
How are we to explain that 032 is closest to texts of Streeter's “Eastern” variety yet is unlike 038? The six-way partition is not inconsistent with Streeter's identification of a distinct textual variety which includes 032, Family 1, 28, the Sinaitic Syriac, Armenian, and Georgian. At the same time, the relevant CMDS map shows that 038 and 565 lie on a trajectory between the Armenian and Georgian versions at one end, and “Western” witnesses at the other. Ironically, it seems that the two manuscripts Streeter regarded as primary authorities for the “Caesarean” sub-variety of his “Eastern” branch are mixtures of “Eastern” and “Western” readings in the Gospel of Mark. Others have already noticed the “Western” leanings of 038 and 565. Larry Hurtado writes, “The quantity of Western readings in Θ and its allies (565, 700) is so great that the present writer would suggest that perhaps the text represented by these MSS is a form of the Western text as it was shaped in the East.” Stephen C. Carlson writes, “The practice of anchoring the 'Caesarean' label on the branch containing Θ and 565 now appears unwise, since Θ and 565 come from a family that originated as a late mixture of Branch gamma (to which Origen’s text belongs) and a Western text substantially similar to D.”[31]
The relevant medoids of the six-way partition, namely the Armenian version and minuscule 205, are better representatives of the textual complex which Streeter called the “Eastern type,” and 032 is closer to these than the other medoids. Whether Gr arm and Gr 205 should be associated with Antioch and Caesarea remains an open question. There has always been a suspicion that the Armenian and Georgian versions trace their ancestry back to the Old Syriac. Syrian Antioch or Edessa would be reasonable guesses for the provenance of the Old Syriac. Making that connection would leave Gr 205 (i.e. Family 1) as a candidate for the “Caesarean” branch of Streeter's “Eastern” text.[32]
The next preferred number of groups is eleven:
Table 21. PAM result (UBS4, eleven groups)
| Medoid | Members |
|---|---|
| 03 | UBS 01 03 044 2427 |
| Byz | 02 f-13 33 157 180 579 597 700 1006 1010 1071 1241 1243 1292 1342 1424 1505 Byz 07 09 011 013 022 042 Lect syr-p syr-h slav |
| 037 | 04 019 037 |
| it-ff-2 | 05 it-a it-b it-c it-d it-ff-2 it-i it-r-1 |
| 032 | 032 |
| 038 | 038 565 syr-pal |
| 205 | f-1 28 205 |
| cop-bo | 892 cop-sa cop-bo |
| vg | it-aur it-f it-l it-q vg eth Augustine |
| it-k | it-k |
| arm | syr-s arm geo |
| Poorly classified (worst last): eth 892 019 | |
When a data set is split into two different numbers of groups, first a smaller then a larger number, it sometimes happens that groups present in the first partition remain substantially unchanged in the second. Such groups are more coherent than others, tending not to fragment. Less coherent groups lose members or split into pieces. Cases which have migrated out of one group might combine with others to form a new group in the second partition while other cases form singletons. Examples of these phenomena are seen by comparing the six- and eleven-way partitions. Gr Byz, Gr it-ff-2, Gr 205, and Gr vg are coherent, remaining much the same when the data set is split into a larger number of groups, although they do lose some of their constituents. Gr 03 (6) and Gr arm (6) (i.e. Groups 03 and arm of the six-way partition) fragment in the eleven-way partition. Gr 03 (6) splits into three parts: a smaller Gr 03 (11) with the same core as its parent; Gr 037, which picks up 04 as well; and Gr cop-bo, which gains 892. Gr arm (6) loses 032 and 565, leaving behind syr-s, arm, and geo. More eccentric witnesses such as 032 and it-k are the first to form singletons. Gr 038, comprised of 038, 565, and syr-pal, forms from cases which have migrated out of other groups. There is a good deal of overlap between Streeter's “Eastern” category and Gr 038, Gr 205, and Gr arm of the eleven-way partition.
Using PAM analysis to divide the UBS4 data set into the next preferred number of twenty-four groups produces this result:
Table 22. PAM result (UBS4, twenty-four groups)
| Medoid | Members |
|---|---|
| 03 | UBS 03 2427 |
| 01 | 01 |
| Byz | 02 33 157 180 597 1006 1010 1071 1241 1243 1292 1424 1505 Byz 07 09 011 013 022 042 Lect syr-p syr-h slav |
| 04 | 04 |
| it-d | 05 it-a it-d |
| 044 | 019 044 892 |
| 032 | 032 |
| 037 | 037 |
| 038 | 038 565 |
| f-1 | f-1 205 |
| f-13 | f-13 |
| 28 | 28 |
| 579 | 579 |
| 700 | 700 |
| 1342 | 1342 |
| vg | it-aur it-f it-l it-q vg Augustine |
| it-i | it-b it-ff-2 it-i it-r-1 |
| it-c | it-c |
| it-k | it-k |
| syr-pal | syr-pal |
| syr-s | syr-s |
| cop-bo | cop-sa cop-bo |
| arm | arm geo |
| eth | eth |
| No negative silhouette widths. | |
This partition has a claim to being the most “natural” one because the corresponding MSW plot has a large magnitude for this number of groups despite the general tendency for MSW values to decrease as the number of groups increases. If this is the best partition then it is reasonable to describe the UBS4 data set as comprised of many small groups and singletons along with a few larger groups such as Gr Byz, Gr vg, and Gr it-i. Most of the other structures present for smaller numbers of groups have fragmented.
The process of division into ever larger numbers of groups could be continued although not much would be gained by doing so. The main contours of the data set's group structure have already been revealed by examining partitions with smaller numbers of groups.
The MSW plot for the INTF data set displays a series of peaks, each indicating a preferred number of groups for partitioning. The plot for the corresponding control indicates the noise level for each number of groups. Comparison shows that each peak in the primary example's MSW plot is worth considering, with one exception. The sole exception is the peak for the maximum possible number of 151 groups. As in the UBS4 data set, division into too many groups produces fairly uninteresting partitions comprised mainly of small groups or singletons. Much of the group structure is revealed by partitions based on the first four peaks in the MSW plot, which occur at two, four, seven, and seventeen groups.
A two-way partition produces Gr A and Gr 1339. The medoid of the first group is the Ausgangstext (i.e. initial text) which represents the text printed in editions such as the INTF Editio Critica Maior, the Nestle-Aland Novum Testamentum Graece, and the UBS Greek New Testament. It is joined by a number of manuscripts which might be described as some flavour of “Alexandrian,” although not many would place 05 (Codex Bezae) in this traditional category. As it happens, 05 has a negative silhouette width for this partition, indicating a poor fit in Gr A. Gr 1339 is broad, containing many witnesses often characterized as “Byzantine” along with others which are not.
Table 23. PAM result (INTF, two groups)
| Medoid | Members |
|---|---|
| A | 01 019 03 037 04 044 05 1342 33 579 892 A |
| 1339 | 011 013 017 02 021 0211 022 028 030 031 032 033 034 036 038 041 042 043 045 047 07 09 1 1009 1012 1071 1093 1110 118 1230 124 1241 1253 1273 1279 1296 13 130 131 1326 1328 1329 1330 1331 1333 1334 1335 1336 1337 1338 1339 1340 1341 1343 1344 1345 1346 1347 1348 1421 1424 1446 1451 1457 150 1500 1502 1506 1528 1555 157 1574 1579 1582 1593 16 1602 1604 1661 1675 1692 174 176 1780 18 1823 184 191 205 209 2193 22 222 233 2372 2411 2542 2546 2680 2726 273 2737 2766 2786 28 3 31 346 348 35 372 4 427 517 543 555 565 61 69 700 713 732 740 752 788 79 791 792 807 826 827 828 829 851 863 954 968 979 983 |
| Poorly classified: 05 | |
In a four-way partition, Gr A remains static while Gr 1339 spawns Gr 209 and Gr 826. These last two largely correspond to Families 1 and 13, respectively. It is interesting to see that Gr 209 contains 032 and that Gr 826 includes 038 and 565. Codex Bezae (05) remains in Gr A but again has a negative silhouette width to indicate a poor fit.
Table 24. PAM result (INTF, four groups)
| Medoid | Members |
|---|---|
| A | 01 019 03 037 04 044 05 1342 33 579 892 A |
| 1339 | 011 013 017 02 021 0211 022 028 030 031 033 034 036 041 042 043 045 047 07 09 1009 1012 1071 1093 1110 1230 1241 1253 1273 1279 1296 130 131 1326 1328 1329 1330 1331 1333 1334 1335 1336 1337 1338 1339 1340 1341 1343 1344 1345 1346 1347 1348 1421 1424 1446 1451 1457 150 1500 1502 1506 1528 1555 157 1574 1579 1593 16 1602 1604 1661 1675 1692 174 176 1780 18 1823 184 191 22 222 233 2372 2411 2546 2680 2726 273 2737 2766 2786 3 31 348 35 372 4 427 517 555 61 700 713 732 740 752 79 791 792 807 827 829 851 863 954 968 979 |
| 209 | 032 1 118 1582 205 209 2193 2542 28 |
| 826 | 038 124 13 346 543 565 69 788 826 828 983 |
| Poorly classified: 05 | |
In a seven-way partition, Gr A, Gr 209, and Gr 826 recur almost unchanged. Codex Bezae (05) is still located in the A group, and still has a negative silhouette width to indicate a poor fit. Codex 032 is again included in Gr 209 (i.e. Family 1). Gr 1339 retains a coherent core and continues to produce new groups, namely Gr 041, Gr 517, and Gr 1528.
Table 25. PAM result (INTF, seven groups)
| Medoid | Members |
|---|---|
| A | 01 019 03 037 04 044 05 1342 33 579 892 A |
| 1339 | 011 013 021 0211 022 028 030 031 033 036 042 043 045 047 07 09 1009 1012 1093 1110 1230 1253 1273 1296 130 131 1326 1328 1329 1330 1331 1333 1334 1335 1336 1337 1338 1339 1340 1341 1343 1344 1345 1347 1348 1446 1451 1457 150 1502 1506 1555 157 1574 1593 1604 1661 1692 174 176 18 1823 191 22 233 2372 2546 2680 273 2737 2766 2786 3 31 35 372 4 427 713 740 79 791 792 807 827 851 968 979 |
| 041 | 017 02 034 038 041 1071 1346 1421 1500 1602 1780 222 2411 732 752 863 |
| 209 | 032 1 118 1582 205 209 2193 2542 28 |
| 826 | 124 13 346 543 69 788 826 828 983 |
| 517 | 1241 1424 1675 517 954 |
| 1528 | 1279 1528 1579 16 184 2726 348 555 565 61 700 829 |
| Poorly classified (worst last): 565 28 05 33 038 118 2766 752 034 427 | |
Gr A, Gr 041, Gr 209, Gr 826, Gr 517, and Gr 1528 remain substantially the same when the data set is divided into the next preferred number of seventeen parts. They are not precisely the same, however. For example, manuscripts 33 and 579 drop out of Gr A (7) to form Gr 579 while manuscripts 732 and 863 of Gr 041 (7) combine with 427 of Gr 1339 (7) to form Gr 732. Also, 034 migrates to Gr 07, and 038 combines with 565 from Gr 1528 (7) to form Gr 565. Gr 1339 (7) begets Gr 07, Gr 022, and Gr 1457. Gr 07 is almost as large as what remains of Gr 1339. Gr 022 contains two deluxe manuscripts dated to the sixth century (i.e. 022 and 042). Minuscules 1071, 1273, and 2766 also move into this group although negative silhouette widths imply a poor fit for 1071 and 1273. Looking at the corresponding CMDS map shows that the singletons for this partition, namely 05, 032, 28, and 792, are somewhat isolated in textual space. Many of the poorly classified manuscripts would move into other groups or singletons if the data set were divided into yet more pieces.
Table 26. PAM result (INTF, seventeen groups)
| Medoid | Members |
|---|---|
| A | 01 019 03 037 04 044 1342 892 A |
| 07 | 011 013 028 031 033 034 036 045 047 07 09 1009 1093 1110 1296 131 1333 1335 1338 1341 1343 1347 1348 1555 1604 1661 174 176 22 2372 273 2786 3 31 4 700 807 851 |
| 041 | 017 02 041 1346 1421 1500 1602 1780 222 2411 752 |
| 1339 | 021 0211 030 043 1012 1230 1253 130 1326 1328 1329 1330 1331 1334 1336 1337 1339 1340 1344 1345 1451 150 1502 1506 157 1574 1692 18 233 2546 2680 2737 35 372 713 740 79 791 968 979 |
| 022 | 022 042 1071 1273 2766 |
| 032 | 032 |
| 565 | 038 565 |
| 05 | 05 |
| 209 | 1 118 1582 205 209 2193 2542 |
| 826 | 124 13 346 543 69 788 826 828 983 |
| 517 | 1241 1424 1675 517 954 |
| 1528 | 1279 1528 1579 16 184 2726 348 555 61 829 |
| 1457 | 1446 1457 1593 1823 191 827 |
| 28 | 28 |
| 579 | 33 579 |
| 732 | 427 732 863 |
| 792 | 792 |
| Poorly classified (worst last): 0211 713 1345 030 1348 1338 1692 1071 1009 1273 2546 1344 2680 1012 791 31 157 130 1336 1502 1340 150 034 021 752 | |
A number of these complexes are already known, as shown in the following table which associates groups discovered by PAM analysis with ones mentioned in Frederik Wisse's book on manuscript classification:[33]
Table 27. Association with known groups
| PAM group | von Soden | Wisse | Other names |
|---|---|---|---|
| Gr A | H | Group B | Alexandrian |
| Gr 07 | Kx | Group Kx | Byzantine |
| Gr 041 | Ka | Group Π | Family Π |
| Gr 1339 | Kr | Group Kr | Byzantine |
| Gr 209 | Iη | Group 1 | Family 1 |
| Gr 826 | Iι | Group 13 | Family 13 |
| Gr 517 | Iφa | Cluster 1675 | Family 1424 |
| Gr 1528 | Iβ | Groups 16, 1216 | |
| Gr 1457 | Cluster 827 |
Finally, dividing into a really large number of parts reveals group cores. Singletons have been omitted from the following list to leave only those sets with more than one member. It is interesting to see that seven of the ten core members of Gr 1339 are from the Saba monastery near Jerusalem. In this group at least, there is a strong correlation between locality and text.[34]
Table 28. Groups cores (INTF, 93 groups, singletons omitted)
| Medoid | Members |
|---|---|
| 031 | 011 013 028 031 033 045 07 09 1110 1296 1341 1343 1347 150 22 3 |
| 041 | 017 041 1346 1500 1602 2411 |
| 022 | 022 042 |
| 1333 | 030 1333 |
| 1421 | 034 1421 |
| 1 | 1 1582 205 209 2193 |
| 1451 | 1012 1451 968 |
| 1230 | 1230 233 |
| 826 | 13 346 543 69 788 826 828 |
| 1339 | 130 1328 1329 1331 1334 1336 1339 1345 18 35 |
| 1338 | 1338 2546 31 |
| 1528 | 1528 1579 16 |
| 517 | 1675 517 |
| 829 | 184 2726 348 829 |
| 791 | 2372 791 |
| 4 | 273 4 |
| 372 | 2737 372 |
| 732 | 427 732 |
| 61 | 555 61 |
Analysis has so far focussed on entire data sets, excluding only as many cases (i.e. witnesses) as necessary to maintain a tolerable level of sampling error. Sometimes, however, it is worthwhile to narrow the scope of analysis to a subset or slice of an original data set. Such a slice might consist of a subset of cases, variables, or both. In terms of a data matrix based on New Testament textual information, a case-wise slice selects particular witnesses while a variable-wise slice selects particular variation units.
In order to reduce sampling error to a tolerable level, the analytical procedures used in this article drop a witness if including it would cause any distance to be calculated from less than fifteen places of comparison. Unfortunately, this policy causes certain witnesses whose readings are not defined at every variation unit to be excluded from consideration. In the present context of New Testament data sets, a number of circumstances can cause the reading of a witness to be undefined at a variation site:
-
A manuscript may be illegible at the relevant place
-
The text preferred by a Church Father may not be discernible due to absence or ambivalence of relevant patristic evidence at the site
-
The Greek reading supported by a version may not be discernible because a back-translation of the relevant passage is consistent with more than one of the Greek alternatives.
One such witness is P45, a third century papyrus manuscript which, due to its fragmentary state, has not yet appeared in the analysis results presented in this article. Happily, its textual nature can be explored by restricting analysis to places where its text is legible.[35]
The MSW plots for both the UBS4 and INTF distance matrices which include P45 have prominent peaks corresponding to four groups. Dividing into this many parts produces these partitions:
Table 30. PAM result with P45 (UBS4, four groups)
| Medoid | Members |
|---|---|
| 03 | UBS 01 03 019 037 2427 cop-bo |
| f-1 | P45 032 038 f-1 28 205 565 syr-s arm geo |
| Byz | 02 f-13 33 157 180 579 597 700 892 1006 1010 1071 1241 1243 1292 1342 1424 1505 Byz 07 09 011 013 042 Lect it-aur it-f it-l vg syr-p syr-h eth slav |
| it-ff-2 | 05 it-a it-b it-c it-d it-ff-2 it-i it-q |
| Poorly classified: 892 | |
Table 31. PAM result with P45 (INTF, four groups)
| Medoid | Members |
|---|---|
| A | 01 019 03 037 04 05 1342 33 579 892 A P45 |
| 1339 | 011 013 017 02 021 0211 022 028 030 031 033 034 036 041 042 043 045 047 07 09 1009 1012 1071 1093 1110 1230 1241 1253 1273 1279 1296 130 131 1326 1328 1329 1330 1331 1333 1334 1335 1336 1337 1338 1339 1340 1341 1343 1344 1345 1346 1347 1348 1421 1424 1446 1451 1457 150 1500 1502 1506 1528 1555 157 1574 1579 1593 16 1602 1604 1661 1675 1692 174 176 1780 18 1823 184 191 22 222 233 2372 2411 2546 2680 2726 273 2737 2766 2786 3 31 348 35 372 4 427 517 555 61 700 713 732 740 752 79 791 792 807 827 829 851 863 954 968 979 |
| 209 | 032 1 118 1582 205 209 2193 2542 28 |
| 826 | 038 124 13 346 543 565 69 788 826 828 983 |
| Poorly classified (worst last): 05 33 P45 | |
The four-way partition of the UBS4 data set places P45 in Gr f-1 with 032, 038, f-1, 28, 205, 565, the Sinaitic Syriac, Armenian, and Georgian. Streeter regarded all of these as members of his “Eastern” category.[36] The four-way partition of the INTF data set places P45 in Gr A, although a negative silhouette width indicates that it is not a good fit there. The CMDS map derived from the INTF distance matrix which includes P45 locates this manuscript approximately the same distance from Gr A, Gr 209, and Gr 1339. Ranking witnesses by distance from P45 using the same distance matrix produces this ordered list:
Table 32. Ranked distances from P45 (INTF, Mark)
| A (0.220); 04 (0.222); 032 (0.237); 028 (0.241); 030 (0.254); 1012 (0.254); 1328 (0.254); 1339 (0.254); 1343 (0.254); 1451 (0.254); 150 (0.254); 18 (0.254); 3 (0.254); 35 (0.254); 517 (0.254); 954 (0.254); 031 (0.263); 047 (0.265); 011 (0.271); 017 (0.271); 034 (0.271); 045 (0.271); 09 (0.271); 1110 (0.271); 118 (0.271); 1273 (0.271); 1296 (0.271); 130 (0.271); 1326 (0.271); 1329 (0.271); 1333 (0.271); 1334 (0.271); 1347 (0.271); 1502 (0.271); 157 (0.271); 1602 (0.271); 22 (0.271); 2680 (0.271); 2766 (0.271); 28 (0.271); 752 (0.271); 791 (0.271); 807 (0.271); 892 (0.271); 1338 (0.273); 2546 (0.273); 1421 (0.286); 013 (0.288); 02 (0.288); 021 (0.288); 036 (0.288); 041 (0.288); 043 (0.288); 07 (0.288); 1 (0.288); 1230 (0.288); 131 (0.288); 1330 (0.288); 1341 (0.288); 1344 (0.288); 1346 (0.288); 1506 (0.288); 1555 (0.288); 1582 (0.288); 176 (0.288); 184 (0.288); 191 (0.288); 2193 (0.288); 233 (0.288); 2372 (0.288); 2411 (0.288); 2542 (0.288); 2737 (0.288); 372 (0.288); 700 (0.288); 79 (0.288); 968 (0.288); 0211 (0.291); 31 (0.296); 1337 (0.298); 022 (0.300); 851 (0.304); 03 (0.305); 042 (0.305); 1071 (0.305); 1093 (0.305); 1241 (0.305); 1331 (0.305); 1336 (0.305); 1348 (0.305); 1424 (0.305); 1500 (0.305); 1528 (0.305); 1675 (0.305); 1692 (0.305); 205 (0.305); 209 (0.305); 222 (0.305); 2786 (0.305); 348 (0.305); 713 (0.305); 740 (0.305); 788 (0.305); 829 (0.305); 863 (0.305); 979 (0.305); 1009 (0.309); 033 (0.321); 038 (0.322); 1335 (0.322); 1342 (0.322); 1345 (0.322); 1457 (0.322); 1579 (0.322); 16 (0.322); 1780 (0.322); 2726 (0.322); 4 (0.322); 555 (0.322); 1574 (0.323); 543 (0.328); 037 (0.339); 1253 (0.339); 1279 (0.339); 1340 (0.339); 1661 (0.339); 273 (0.339); 427 (0.339); 61 (0.339); 826 (0.339); 827 (0.339); 828 (0.339); 174 (0.345); 01 (0.356); 13 (0.356); 1593 (0.356); 1604 (0.356); 346 (0.356); 565 (0.356); 69 (0.356); 732 (0.356); 579 (0.362); 019 (0.373); 05 (0.373); 124 (0.373); 1446 (0.373); 1823 (0.373); 792 (0.373); 983 (0.390); 33 (0.392) |
All of these distances are larger than the upper critical limit of the confidence interval of distances which can be attributed to chance. That is, P45 is eccentric by the standard of manuscripts included in the INTF data set, being a long way from any of them. Its nearest neighbours are the synthetic Ausgangstext (A) followed by 04 from Gr A, 032 from Gr 209, then an array of manuscripts from Gr 1339 of the relevant four-way partition. In the context of the INTF data set, it seems reasonable to describe P45 as an isolated text which is roughly the same distance from Gr A, Gr 209, and Gr 1339.
Origen's text is another witness which falls victim to the vetting process, and it too can be included by restricting analysis to an appropriate slice of the data set.[37] Both the CMDS map and DC dendrogram place Origen in the vicinity of witnesses that Streeter styled as “Eastern.”
The corresponding MSW plot indicates that a four-way partition is preferable. When the data set is divided into four, the group occupied by Origen's text includes 038, 28, 565, the Sinaitic Syriac, Armenian, and Georgian. Streeter, aware of the tendency for Origen's citations from the Gospel of Mark to agree with these witnesses, concluded that this kind of text was already established in Caesarea when Origen moved there in 231 and thus provides a “fixed point for the history of the text of the New Testament.”[38]
Table 34. PAM result with Origen (UBS4, four groups)
| Medoid | Members |
|---|---|
| 03 | UBS 01 03 019 032 037 2427 cop-sa cop-bo |
| Byz | 02 f-1 f-13 33 157 180 205 579 597 700 892 1006 1010 1071 1241 1243 1292 1342 1424 1505 Byz 07 09 011 013 042 Lect it-aur it-f it-l vg syr-p syr-h eth slav |
| it-ff-2 | 05 it-a it-b it-c it-d it-ff-2 it-i it-q it-r-1 |
| Origen | 038 28 565 syr-s arm geo Origen |
| Poorly classified (worst last): 892 032 | |
Sometimes the textual affiliation of a witness changes from section to section. One way such block mixture might have occurred is through partial correction of one text to another. A corrector might have begun to “improve” his or her copy by reference to a second text then have lost interest or run out of time before the work was completed. If the corrected text was later copied then that copy and its descendants would contain as many of the second text's readings as had been transferred by the corrector then retained by the copyist. Another way block mixture might have occurred is through replacement of damaged leaves by ones copied from a different variety of text.
Shifts in the textual character of a witness can be studied by first dividing a data matrix into consecutive blocks with approximately equal numbers of variation units, next producing a distance matrix for each block, then performing multivariate analysis on each block's distance matrix. There is a trade-off concerning how many blocks to use. On one hand, shifts which occur in a small section of text have a better chance of being detected if the data set is divided into correspondingly small blocks. On the other hand, sampling error increases as the number of blocks increases because of the decreasing number of variation units in each one. Consequently, increasing the number of blocks also increases the number of fragmentary witnesses that must be excluded to maintain the integrity of analysis results.
Every distance in a distance matrix based on incomplete data is a mere estimate of the actual distance that would be obtained if every place of variation between two witnesses were compared. As it happens, the sampling error of the distance estimate is roughly equal to the square root of the number of places sampled. Thus, if two witnesses are compared at one hundred places and disagree at fifty then the estimated simple matching distance is 50/100 (0.5) and the associated sampling error is approximately equal to the square root of one hundred, which is ten. Consequently, in this example it would not be unlikely for the actual distance to be anywhere between (50 - 10)/100 (i.e. 0.4) and (50 + 10)/100 (i.e. 0.6).
In the CMDS maps, sampling error causes plotted witness locations to be randomly displaced from where they would be given a larger sample. In the DC dendrograms, sampling error can cause witnesses to jump between branches, especially if those witnesses have mixed texts that stand between the textual varieties associated with the branches. One must search for genuine textual shifts against this noisy background, and dividing data sets to search for block mixture only makes matters worse.
Dividing data sets into blocks also creates difficulties for PAM analysis. MSW plots are unlikely to suggest the same number of groups for every block. However, it is desirable to use a single number of groups when comparing group membership across blocks. The chosen number of groups should not be so small that actual shifts will be missed or so large that spurious shifts will occur through sampling error. Despite these difficulties, useful analysis results can be obtained provided that each block retains a sufficient number of variation units. Dividing the UBS4 data matrix into four consecutive blocks of approximately equal size results in each one having about thirty-five variables. This is enough to avoid too many witnesses being dropped due to the constraint on the minimum number of variables required to calculate a distance, which in this study is set to fifteen. The sampling error in distances between witnesses for each block is roughly twice that of distances calculated using the undivided data set covering all of Mark. The factor of two occurs because the data set is divided into four, and four divided by its square root (i.e. two) is two.
The following results are obtained when the UBS4 data set for Mark is divided into four blocks and each is separately analysed:[39]
Comparing the CMDS maps shows that the overall structure of the plots is similar across blocks. However, some texts exhibit substantial shifts in their relative locations. To name a few, Family 1 (f-1), 038, 565, Old Latin Codex Corbeiensis II (it-ff-2), the Ethiopic (eth), and Sahidic Coptic (cop-sa) do not seem to have stable locations across blocks. Each of these shifts is consistent with partial correction of an ancestral text to another standard. For example, the Sahidic is near “Eastern” texts in the first block but near “Alexandrian” ones in the other three blocks. Perhaps the initial text of this Coptic version had an “Alexandrian” flavour throughout but was then partially revised so that it became more “Eastern” in the first few chapters of Mark?
The DC dendrograms also exhibit a similarity of analysis results across blocks with the exception of a few texts which tend to shift from branch to branch. The exceptions are generally the same texts which undergo substantial shifts in the CMDS maps. Codex 032, which is thought to be more “Western” in the initial chapters of Mark, occupies the “Western” branch of the DC dendrogram for the first block.
Partition into a single number of groups is desirable for comparison across blocks using PAM analysis. However, the MSW plots for these blocks do not agree on a single preferred number. To choose what seems a reasonable compromise, partitioning into five groups returns a fairly high MSW value for each block while providing enough slots to allow some differentiation but not so many that like texts are liable to fall into different slots through sampling error.
Table 36. PAM result (Block 1: Mk 1.1-4.24, five groups)
| Medoid | Members |
|---|---|
| 03 | UBS 01 03 019 2427 |
| Byz | 02 04 f-1 33 157 180 205 565 579 597 700 892 1006 1010 1071 1241 1243 1292 1342 1424 1505 Byz 07 09 011 013 042 Lect syr-p syr-h slav |
| it-d | 05 it-a it-b it-d it-e it-ff-2 it-q it-r-1 |
| geo | 032 038 f-13 28 cop-sa arm geo |
| vg | 037 it-aur it-c it-f it-l vg eth |
| Poorly classified (worst last): 28 f-13 037 it-c | |
Table 37. PAM result (Block 2: Mk 4.28-8.15, five groups)
| Medoid | Members |
|---|---|
| 03 | UBS 01 03 019 037 1342 2427 cop-bo |
| Byz | 02 f-13 33 157 180 579 597 1006 1010 1071 1241 1243 1292 1424 1505 Byz 07 09 011 013 042 Lect syr-p syr-h slav |
| it-ff-2 | 05 038 565 it-a it-b it-c it-d it-ff-2 it-i it-q it-r-1 |
| 205 | 032 f-1 28 205 syr-s arm geo |
| vg | 700 892 it-aur it-f it-l vg cop-sa eth |
| Poorly classified (worst last): 700 it-c it-f eth cop-sa 892 | |
Table 38. PAM result (Block 3: Mk 8.26-11.25, five groups)
| Medoid | Members |
|---|---|
| 2427 | UBS 01 03 04 019 037 044 892 2427 it-k cop-sa cop-bo |
| Byz | 02 157 180 597 700 1006 1010 1071 1241 1243 1292 1342 1424 1505 Byz 07 09 011 013 022 042 Lect syr-p syr-h slav |
| it-d | 05 it-a it-b it-d |
| arm | 032 f-1 28 205 syr-s arm geo |
| vg | 038 f-13 565 579 it-aur it-c it-f it-ff-2 it-i it-l it-q vg eth |
| Poorly classified (worst last): it-q 565 f-13 579 eth it-ff-2 it-i | |
Table 39. PAM result (Block 4: Mk 12.23-16.20, five groups)
| Medoid | Members |
|---|---|
| 03 | UBS 01 03 019 044 2427 cop-sa cop-bo |
| Byz | 02 04 037 f-1 f-13 28 33 157 180 205 579 597 700 892 1006 1010 1071 1241 1243 1292 1342 1424 1505 Byz 07 011 013 042 Lect syr-p syr-h eth slav |
| it-d | 05 it-d it-k |
| 565 | 032 038 565 arm |
| vg | it-aur it-c it-ff-2 it-l it-q vg syr-s |
| Poorly classified (worst last): 04 892 syr-s | |
The medoids of some groups change from block to block. Nevertheless, corresponding groups in different blocks are able to be identified because certain witnesses recur within them. In what follows, groups will be labelled by chaining together the sigla of the associated medoids, using a final ellipsis in cases which have three or more medoids across corresponding groups (e.g. Gr geo/205/...).
A few texts such as 04, 044, the Sinaitic Syriac (syr-s), Old Latin k (it-k), and Bohairic Coptic (cop-bo) are not present in every division due to the vetting procedure exercised to reduce sampling error. Nothing can be said about their character in divisions which omit them.[40] It is prudent to also treat poorly classified witnesses (i.e. those with a negative silhouette width) as absent. Excluding these from consideration, a comparison of corresponding groups across blocks helps to identify witnesses that exhibit textual shifts:
Table 40. Textual shifts
| Block | Gr 03/2427 | Gr Byz | Gr it-d/it-ff-2 | Gr geo/205/... | Gr vg |
|---|---|---|---|---|---|
| 1: Mk 1.1-4.24 | 04 f-1 205 565 892 1342 | it-ff-2 it-q | 038 cop-sa | eth | |
| 2: Mk 4.28-8.15 | 037 1342 | 038 565 it-ff-2 it-q | f-1 28 205 | ||
| 3: Mk 8.26-11.25 | 04 037 892 cop-sa | 1342 | f-1 28 205 | 038 | |
| 4: Mk 12.23-16.20 | cop-sa | 04 037 f-1 28 205 1342 eth | 038 565 | it-ff-2 it-q |
Some of these shifts may be due to witnesses being located midway between adjacent groups. When a witness is in such a position, slight perturbations of the distance matrix may cause a jump from one group to another. Inspection of the CMDS maps for the four blocks shows that 04, 892, and 1342 are approximately equidistant from the centres between which they shift. That leaves 037, 038, f-1, 28, 205, 565, Latin codices Monacensis (it-q) and Corbeiensis II (it-ff-2), the Sahidic Coptic, and Ethiopic as texts which appear to exhibit block mixture.
Certain texts adhere to one standard in the first and last blocks but another in between. For example, the entity which represents Family 1 in the UBS apparatus (i.e. f-1) starts and ends as Gr Byz but belongs to Gr geo/205/... in the middle; 038 starts and ends as Gr geo/205/... but changes allegiance to Gr it-d/it-ff-2 or Gr vg in the central parts of Mark. Such witnesses may have resulted from partial efforts to make one text conform to another, cosmetic renovations that affected the outer leaves of a book but left the interior untouched.
PAM analysis does not identify 032 (i.e. Codex W) as a shifting text but instead classifies it as a member of Gr geo/205/... in all four blocks. This is surprising because the first chapters of Mark in 032 have long been considered to preserve a “Western” text. Henry A. Sanders thought the initial part of Mark (up to 5.31) was the Greek equivalent of the Old Latin version, agreeing with Codex Palatinus (it-e) in particular, and noticed an increasing number of agreements with “Syriacising” manuscripts such as Family 1, Family 13, 28, and 565 in the remainder (after 5.31). Streeter compared the part of 032 following Mark 5.31 with members of his “Caesarean” text (i.e. 038; Families 1 and 13; minuscules 28, 565, and 700), and concluded that it is “a member of the Θ family, the text of which has suffered, but not too greatly, from Byzantine revision.”[41]
The DC dendrogram for Mark 1.1-4.24 places 032 in a branch which is safely described as “Western.” The following table, which lists the ten nearest neighbours of 032 in each block, also reveals the “Western” tendency of 032 in the first few chapters of Mark. Codices Palatinus (it-e), Veronensis (it-b), and Bezae (05) are among the nearest neighbours of 032 in the first block. In the remainder of Mark, the nearest neighbours of 032 are predominantly members of Gr geo/205/.... This group, which corresponds to Streeter's “Eastern” text, includes the Armenian, Georgian, and Sinaitic Syriac. It is possible that these versions share the blame for the distinctive text which Greek members of this group, including 032, bear.
Streeter's statement about Byzantine revision needs to be qualified. While there is Byzantine influence in the second block, as attested by the proximity of 02, 011, and 1243, this component disappears in the third and fourth blocks where members of Gr 03/2427 appear instead. None of the listed texts is significantly near 032, as indicated by the asterisks attached to distances. The text of 032 in Mark seems to be isolated yet cosmopolitan, with varying “Eastern,” “Western,” “Byzantine,” and “Alexandrian” components in consecutive blocks.
Table 41. Nearest ten neighbours of 032 by block (UBS4, Mark)
| Block | Witnesses |
|---|---|
| 1: Mk 1.1-4.24 | it-e (0.480*); 042 (0.543*); it-b (0.571*); eth (0.586*); 1292 (0.594*); f-13 (0.600*); arm (0.600*); geo (0.600*); Lect (0.613*); 05 (0.618*) |
| 2: Mk 4.28-8.15 | f-1 (0.486*); 205 (0.486*); f-13 (0.514*); slav (0.531*); syr-p (0.533*); 02 (0.543*); 038 (0.543*); 1243 (0.543*); 011 (0.543*); it-f (0.548*) |
| 3: Mk 8.26-11.25 | arm (0.323*); syr-s (0.370*); cop-sa (0.370*); 019 (0.452*); 037 (0.457*); 205 (0.457*); 044 (0.469*); 28 (0.486*); geo (0.500*); UBS (0.514*) |
| 4: Mk 12.23-16.20 | syr-s (0.375*); f-13 (0.455*); cop-bo (0.458*); 892 (0.469*); 038 (0.484*); 565 (0.500*); f-1 (0.517*); arm (0.519*); 33 (0.538*); syr-h (0.538*) |
There is such a great number of New Testament witnesses that it is often a practical necessity to restrict ones retained in a summary of the evidence to those few which sufficiently represent the many that have to be omitted. The medoids identified by PAM analysis constitute suitable representatives although alternative witnesses must be selected to represent a group when its medoid is absent at some variation sites or is affected by block mixture. The selection procedure begins with a data set which includes as many witnesses as practicable. PAM analysis is performed for every possible number of groups to plot mean silhouette width versus the number of groups. Next, the plot is used to identify a suitable number of groups. PAM analysis is then applied again to partition the data set into the chosen number of groups, identifying the medoids in the process. Just how many groups are selected depends on the purpose. If aiming to produce a compact apparatus then a smaller number would be chosen; a larger number would be appropriate if presenting a comprehensive survey of, say, the Byzantine textual complex. To give an example, the medoids of the eleven-way partition of the UBS4 data set presented above would serve as a useful starting point if seeking representative texts for a compact summary of the textual situation in Mark. As another example, medoids found by a many-way partition of the INTF data set for Mark would be suitable candidates for witnesses that represent the entire spectrum of extant Greek textual varieties of that Gospel.
A multivariate analysis technique called correspondence analysis is able to produce a biplot which simultaneously displays both the cases and variables of a data matrix. This allows variables which are useful for differentiating between cases to be identified, thus providing a basis for classification. If the variables are comprised of categorical data, as is the case for the New Testament textual data analysed in this article, then a technique called multiple correspondence analysis (MCA) should be used. To illustrate, the following biplot is produced by applying MCA to the first section of UBS4 data previously used to investigate block mixture in Mark:[42]
The plot is cluttered by inclusion of a label for every variant of every variation unit in the data set. Nevertheless, it does illustrate the potential of the technique to identify variants which are useful for classification purposes. The best variants to use are those whose vectors (indicated by red arrows in this diagram) have a large magnitude. Some vectors point directly at known groups, making the associated variants especially suitable for identifying members of that group. To illustrate, the correspondence of the witness label 03 (representing Codex Vaticanus) and the vector pointing to the variant labelled Mk.2.22.2.1 (representing the first variant listed at the second variation unit of Mark 2.22 in the UBS4 apparatus) indicates that this variant is a useful test for the kind of text found in this manuscript. If the analysed data contains so many variants that the biplot is impossible to use then the coordinates of witnesses and variants can be printed out to identify variation sites useful for classifying texts. The location of an unknown witness with respect to known groups could be quickly established by comparing the variants it supports with those supported by group medoids at variation sites identified by this procedure.
The quest to discover textual groups among New Testament witnesses has a long history. Although an interesting challenge in its own right, the quest is often motivated by the need for a compact, comprehensive, and comprehensible apparatus for a critical text. As Frederik Wisse says,[43]
Ideally, a critical apparatus gives all pertinent MS evidence necessary for the establishment of the best possible text, and nothing more. Since the number of MSS used in an apparatus must be kept within reasonable limits, it is clear that only a fraction of the total number of Greek MSS of the NT can be included. This could easily lead to arbitrariness — and it often has — unless somehow true representation could be assured. Selection is defensible only if the user of the apparatus can be convinced that the number of MSS presented spans and represents the whole tradition in text, date, and, insofar as this is known, provenance.
It may be that the number of witnesses required to be presented cannot be significantly reduced because the tradition is so diverse that few witnesses are adequately represented by others. However, if presenting a less than comprehensive picture is acceptable, as, say, in a concise summary, then a great reduction in the number of witnesses that need to be presented is certainly achievable. To reduce the clutter and thereby make the presented information more comprehensible, it is necessary to identify witnesses to represent the various complexes that populate the textual landscape. To cover the entire landscape, it is also necessary to include mixed texts which stand between groups and eccentric ones which stand apart.
Prior attempts to find groups, identify representatives, and classify as yet unclassified witnesses of the New Testament often fall into one of two categories. The first is of “quantitative” methods which count agreements with selected witnesses to discover where an unclassified witness lies in relation to them. A weakness of this approach is that the selected witnesses are typically chosen by an ad hoc method, often based on a survey of prior studies. If the text being classified does not belong to any of the groups represented by the selected witnesses then it is likely to be misclassified. The second is of “profile” methods which search for combinations of shared readings. These methods are inductive, relying on an initial phase where many texts are compared to identify variation sites which seem to be useful for discriminating between groups. This approach succeeds in identifying witnesses that belong to groups identified during the initial phase. However, if the initial phase does not cover all extant witnesses, there is a chance that important variation sites for group classification will not be discovered.
Both approaches suffer from a crisis of definition whereby it is unclear how to establish group membership on anything but an arbitrary basis. In profile methods, one has to set a standard for the proportion of group readings which must be supported by a manuscript before it is regarded as a group member. Typically, a proportion (e.g. two-thirds) is simply stated but no analytical basis for the criterion is provided. Similarly, quantitative methods declare critical values which must be satisfied for a witness to be regarded as a group member without performing the statistical analysis necessary to decide which values are appropriate for the data set. For example, Colwell and Tune propose that “the quantitative definition of a text-type is a group of manuscripts that agree more than 70% per cent of the time and is separated by a gap of about 10 per cent from its neighbours.”[44] As shown above, what constitutes a statistically significant level of agreement varies from one data set to the next. Also, mixture among texts and the great number of surviving witnesses mean that one cannot expect to find large gaps in levels of agreement between members of neighbouring textual groups.[45] While Colwell and Tune's quantitative definition of a text-type may have been appropriate for the data set they were using, it is not suitable for general application. Studies which have used this definition or a variation upon it (e.g. requiring less than 70% agreement) may have reached erroneous conclusions about grouping among witnesses, either missing statistically significant levels of agreement or asserting that relationships exist when the associated levels of agreement can be attributed to chance.
The multivariate analysis methods used in this article provide robust ways to identify where a text lies in relationship to others. They are useful for comprehending the broad outlines of the textual space constituted by the witnesses. Classical multidimensional scaling reveals groups of varying scope and density formed by extant texts. It locates member texts within, mixed texts between, and eccentric texts outside extant groups. Divisive clustering gives a complementary presentation of what Bengel called the companies, families, tribes, and nations formed by New Testament witnesses. Partitioning around medoids allows a data set to be divided into groups, and the mean silhouette width indicates which numbers of groups are the more natural. PAM analysis also identifies a medoid for each group, namely that witness standing nearest to the centre of its group. As such, the medoid is often a suitable representative of its group although an alternative may need to be found if, say, the medoid is fragmentary or is not a Greek manuscript. PAM analysis thus provides a way to identify preferable numbers of groups, partition witnesses into those numbers of groups, and identify a representative of each group.
These multivariate analysis techniques are rooted in sound statistical reasoning. If they give a vague result concerning some question then it is possible that the data set being analysed does not contain the information required to give a more definite answer. However, analysis of a more comprehensive data set may still leave the question unanswered. For example, no amount of further information will help decide which group a text belongs to if it has a mixture of readings taken from differing groups. All that can be said is where such a text lies in relation to those groups whose readings it contains.
In their Introduction, Westcott and Hort say that “all trustworthy restoration of corrupted texts is founded on the study of their history, that is, of the relations of descent or affinity which connect the several documents.”[46] The multivariate analysis techniques used in this article do not seek to discover relations of descent among the textual states represented by the various witnesses. However, they do show how texts relate to one another with respect to affinity. A comparison of data sets based on variation sites among New Testament witnesses with control data sets which have no relationships among their cases shows that the New Testament textual tradition has a definite group structure which is consistent with there being a number of textual varieties. It is not easy to say how many varieties there are, however. The lack of a clearly preferred number is implied by lack of a clearly preferable peak in a typical plot of mean silhouette width versus the number of groups. Nevertheless, some numbers of groups are more preferable than others; they reflect more “natural” divisions of a data set.
Partitioning the UBS4 data set for the Gospel of Mark into a small number of groups results in divisions which correspond fairly well to conventional “Byzantine,” “Alexandrian,” and “Western” types. There is also a distinct group corresponding to Streeter's “Eastern” type which counts the Old Syriac, Armenian, Georgian, P45, W, Family 1, minuscule 28, and Origen's quotations of Mark among its affiliates. Codex Koridethi (038) and minuscule 565, which Streeter regarded as primary authorities for his “Caesarean” text, actually seem to be mixtures of the “Western” and “Eastern” varieties. Another cluster corresponds to Jerome's Vulgate version of Mark's Gospel. It is located directly between a group of Old Latin texts and the “Byzantine” cluster, suggesting that the “early” Greek manuscripts Jerome used to revise the Latin text were of the “Byzantine” variety.
An interesting feature of the analysis results based on the UBS4 data set is the collocation of early versions of the New Testament with some of the major textual branches: Coptic versions are associated with the “Alexandrian” branch; Latin versions with the “Western;” and the Old Syriac, Armenian, and Georgian with the “Eastern.” This might be construed as evidence that these early versions played a part in the textual tradition's divergence into the associated varieties.
The INTF data set is more comprehensive with respect to Greek manuscripts. Analysis of this data set reveals a number of the same groups found when the UBS4 data set is analysed although there are notable differences as well. A number of the groups identified by PAM analysis of the INTF data set correspond to ones which have been noticed in prior studies. Core members are revealed by partitioning the data set into a large number of groups. In the group core which has minuscule 1339 as its medoid, seven out of ten manuscripts are from the same monastery. In this case at least, the textual character of a group correlates with the provenance of its members.
Aland, Barbara, Kurt Aland, Johannes Karavidopoulos, Carlo M. Martini, and Bruce M. Metzger, eds. The Greek New Testament. 4th rev. ed. Stuttgart: United Bible Societies, 1983.
Aland, Barbara, Kurt Aland, Gerd Mink, Holger Strutwolf, and Klaus Wachtel, eds. Novum Testamentum Graecum: Editio Critica Maior. Stuttgart: German Bible Society, 1997-.
Anderson, Amy S. “Codex 1582 and Family 1 of the Gospels: The Gospel of Matthew.” PhD diss., University of Birmingham, 1999.
Carlson, Stephen C. “The Origin(s) of the 'Caesarean' Text.” Paper presented at the annual meeting of the Society of Biblical Literature, San Antonio, 2004.
Colwell, Ernest C. and Ernest W. Tune. "Method in Establishing Quantitative Relationships between Text-Types of New Testament Manuscripts." In Studies in Methodology in Textual Criticism of the New Testament, New Testament Tools and Studies 9, 56-62. Leiden: Brill, 1969.
Finney, Timothy J. “The Ancient Witnesses of the Epistle to the Hebrews.” PhD diss., Murdoch University, 1999. http://purl.org/tfinney/PhD/
———. “Mapping Textual Space.” TC: A Journal of Textual Criticism 15 (2010). http://purl.org/TC/v15/Mapping/
———. “Analysis of Textual Variation.” Informal publication, 2011. http://purl.org/tfinney/ATV/
Hurtado, Larry W. Text-Critical Methodology and the Pre-Caesarean Text: Codex W in the Gospel of Mark. Studies and Documents 43. Grand Rapids: Eerdmans, 1981.
Jerome. Epistula ad Damasum. In The Principal Works of St. Jerome, translated by W. H. Fremantle, 487-8. Nicene and Post-Nicene Fathers, series 2, vol. 6, ed. P. Schaff. New York: Christian Literature, 1892. http://www.ccel.org/ccel/schaff/npnf206.vii.ii.viii.html
Maechler, M., P. Rousseeuw, A. Struyf, and M. Hubert, and K. Hornik. “Cluster Analysis Basics and Extensions.” Program documentation for the “cluster” package of R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing, 2011.
Metzger, Bruce M. The Early Versions of the New Testament: Their Origin, Transmission, and Limitations. Oxford: Clarendon, 1977.
Mink, Gerd. “Problems of a Highly Contaminated Tradition: The New Testament.” In Studies in Stemmatology II, edited by P. van Reenen, A. den Hollander, and M. van Mulken, 13-85. Amsterdam: John Benjamins, 2004.
Mullen, Roderic L. The New Testament Text of Cyril of Jerusalem. New Testament in the Greek Fathers 7. Atlanta: Society of Biblical Literature, 1997.
R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing, 2011. http://www.r-project.org/
Richards, W. L. The Classification of the Greek Manuscripts of the Johannine Epistles. SBL Dissertation Series 35. Missoula: Scholars Press, 1977.
Sanders, Henry A. The Washington Manuscripts of the Four Gospels in the Freer Collection. New York, Macmillan, 1912.
Spencer, Matthew, Klaus Wachtel, and Christopher J. Howe. “The Greek Vorlage of the Syra Harclensis: A Comparative Study on Method in Exploring Textual Genealogy.” TC: A Journal of Textual Criticism 7 (2002). http://purl.org/TC/v07/SWH2002/
Streeter, Burnett Hillman. The Four Gospels: A Study of Origins Treating of the Manuscript Tradition, Sources, Authorship, and Dates. 8th impression. London: Macmillan, 1953.
Strutwolf, Holger and Klaus Wachtel, eds. Novum Testamentum Graecum: Editio Critica Maior: Parallel Pericopes: Special Volume Regarding the Synoptic Gospels. Stuttgart: German Bible Society, 2011.
Thorpe, J. C. “Multivariate Statistical Analysis for Manuscript Classification.” TC: A Journal of Textual Criticism 7 (2002). http://purl.org/TC/v07/Thorpe2002.html
Venables, William N. and Brian D. Ripley. Modern Applied Statistics with S. 4th ed. New York: Springer, 2002.
Wachtel, Klaus. "Colwell Revisited: Grouping New Testament Manuscripts." In The New Testament Text in Early Christianity: Proceedings of the Lille Colloquium, July 2000, Histoire du texte biblique 6, 31-43. Lausanne: Editions du Zèbre, 2003.
———. "Conclusions." In The Textual History of the Greek New Testament: Changing Views in Contemporary Research, edited by Klaus Wachtel and Michael W. Holmes, 217-26. Text-Critical Studies 8. Atlanta: Society of Biblical Literature, 2011.
Westcott, B. F. and F. J. A. Hort. The New Testament in the Original Greek. Vol. 2. Introduction [and] Appendix. London: Macmillan, 1881.
[1] My “Analysis of Textual Variation” describes how to prepare data extracted from a critical apparatus for analysis and compares results obtained when various MVA techniques are then applied; my PhD dissertation, “Ancient Witnesses,” applies multivariate analysis to full transcriptions of early manuscripts of the Epistle to the Hebrews; “Mapping Textual Space” presents analysis results based on data extracted from a critical apparatus of Hebrews. J. C. Thorpe, “Manuscript Classification,” provides another introduction to multivariate analysis of data relating to New Testament textual variation.
[2] Maechler and others, “Cluster Analysis Basics and Extensions,” “diana” method of the “cluster” package.
[3] For examples of phylogenetic analysis results see Spencer, Wachtel, and Howe, “The Greek Vorlage of the Syra Harclensis.”
[4] See the R Project for Statistical Computing. All R scripts used while preparing this article are available at http://purl.org/tfinney/Groups/scripts/.
[6] The function that
performs random selection needs to be supplied with the probability of the first state
being selected. This is calculated using the expression prob = (1 +
(1 - 2*d)^0.5) / 2, where prob is the probability of
the first state and d is the desired mean distance. In the
limit of an infinite number of cases, using this probability would produce the desired
mean distance.
[7] Aland and others, eds., Greek New Testament, 4th ed.
[8] Strutwolf and Wachtel, eds., Parallel Pericopes. While most texts relate to the first hand of a Greek manuscript, others record supplementary, corrected, alternative, additional, and commentary readings. See the “Introduction,” 5*-7*, for a complete description. The electronic file is located at http://intf.uni-muenster.de/PPApparatus/.
[9] See the chart on page 108 of Streeter's Four Gospels for lists of witnesses that he regarded as primary, secondary, and tertiary authorities of the “Caesarean” text.
[10] Jerome, Epistula ad Damasum, translated by W. H. Fremantle.
[11] Gerd Mink, "Problems of a Highly Contaminated Tradition," page 20 and note 20. This table excludes 59 variation units which have only one reading among the Greek manuscripts examined. These 59 identify places where variations in the Greek text are implied by lectionaries, patristic citations, and versions.
[12] Wachtel, “Conclusions,” 221.
[13] Mink, "Problems of a Highly Contaminated Tradition," 22.
[14] An alpha value of 5% is common for work where the consequences of false positives are not too dire.
[15] These values were
computed with the R expression qbinom(c(0.025, 0.975), n, p)/n, where n is the number of trials and p is the
probability of success. The values 0.025 and 0.975 are the upper and lower quantiles, which specify the probability of a random
variable being less than the corresponding limit. The difference between these quantiles
is 0.95, the complement of the alpha value.
[16] The R script named hist.r was used to produce the histogram and binomial curve in each case. The mean number of variation units is rounded because the number of trials used to define a binomial distribution must be an integer. Each binomial curve has been scaled up to the maximum height of the corresponding histogram; if not scaled, the vertical height is much less, making it more difficult to see the horizontal limits implied by the binomial distribution. Due to the scaling, the vertical scale does not give probability values for the binomial curves.
[17] The critical limits were obtained with the same R script as used to produce the histograms and binomial curves (i.e. hist.r). The relevant R expression is the same as was used to obtain critical limits for the simple model. There, the probability value was 0.5; here, it is the mean distance.
[18] The limit is obtained
using the R expression qbinom(alpha/2, n,
p)/n, where the alpha value is 0.05, the number of trials (n) is 15, and the
probability of success (p) is 0.481.
[19] The R script named sampling.r was used to produce these values. It randomly selects the
requested number of variables then compares them for the two cases specified. The
estimated distance is the simple matching distance between the two cases obtained by
counting the number of disagreements and dividing by the number of places compared. The
limits are obtained with the expression qbinom(c(alpha/2, 1 -
alpha/2), n, p)/n, where alpha, n, and p are the alpha value (i.e. 0.05 in this article),
number of trials (i.e. the number of places compared), and probability (i.e. the
estimated distance). Three decimal places are given for all of the values even though
this level of precision may be unwarranted in view of the confidence interval.
[20] The magnitude of the
margin of error for simple matching distances and the binomial distribution is
approximately (t * (p * (1 - p))^0.5) / n^0.5, where t is the
appropriate t-distribution value, p the
probability, and n the number of trials. The value of t tends towards the corresponding
z value for the normal distribution (e.g. 1.96 for an alpha value of 0.05) as the number of trials
increases. For smaller values of n, the t value may be obtained using the R expression qt(1 - alpha/2, df=n-1).
Taking the seventh row of the table as an example, when n is 50 and the alpha value is 0.05 then
the t value is 2.01. Taking the estimated distance (0.22) as the probability produces a
margin of error estimate of (2.01 * (0.22 * 0.78)^0.5) /
50^0.5, which is 0.118. This agrees quite well with the margins of 0.10 (lower)
and 0.12 (upper) obtained with the binomial distribution.
[21] This list was produced by the R script named rank.r. The confidence interval used to decide whether each distance is statistically significant was calculated using an alpha value of 0.05, the number of variation units where the corresponding witness is defined, and the rounded mean distance between all pairs of witnesses.
[22] This assumes that the entity used to represent Family 1 in the UBS4 apparatus (i.e. f-1) does represent that family of texts.
[23] These diameters were estimated by inspection of the CMDS maps for the UBS4 and INTF control data sets.
[24] If grouping is particularly well defined then there is no need to apply multivariate analysis techniques because it is straightforward to identify the groups by inspection of the data or distance matrix. An abuse such as grouping unrelated cases by means of divisive clustering casts the researcher in a poor light, not the analysis method. Embarrassment might be avoided by knowing the data and the limitations of each analysis technique.
[25] Maechler and others, “Cluster Analysis Basics and Extensions,” “pam” method of the “cluster” package.
[26] Frederik Wisse introduced group labels comprised of a “Gr” prefix and manuscript siglum in his Profile Method for Classifying and Evaluating Manuscript Evidence.
[27] The dates are taken from Aland and others, eds., The Greek New Testament, 26*-28*. I do not mean to say that the Palestinian Syriac and Ethiopic versions are primarily translations of the Vulgate! According to Metzger, Early Versions, 82, “the text of the Palestinian Syriac version agrees with no one type of text, but embodies elements from quite disparate families and texts.” Rochus Zuurmond, “The Ethiopic Version,” 146, writes, “Whatever the vicissitudes of the Eth may have been, and granted that influences from non-Greek sources may have played their role already at an early stage, the Eth is an immediate descendant of the Greek textual tradition.”
[28] Streeter, Four Gospels, 27. Witnesses that Streeter regards as members of each sub-variety are listed in his chart of MSS. and Local Texts (108). Kirsopp Lake identified minuscule 205 as a member of Family 1. Manuscripts 023 and 039 do not include the Gospel of Mark. The Armenian version appears in the columns for both Antioch and Caesarea. Streeter (104) suggests that the Old Armenian, which possibly had been translated from the Old Syriac in the first place (76), was later revised against manuscripts of the Caesarean variety. Roderic L. Mullen surveys quests for a Palestinian variety of the text in his New Testament Text of Cyril of Jerusalem, 29-59.
[29] Hurtado, Text-Critical Methodology, 83.
[30] Hurtado, Text-Critical Methodology, 19; Streeter, Four Gospels, 69. The ranked list was produced using the R script named rank.r. It uses a distance matrix constructed from a data matrix which only includes Mark chapters 6-16. Distances marked by an asterisk are not unlikely to occur for pairs of cases whose states have been randomly selected from those available.
[31] Hurtado, Text-Critical Methodology, 88; Carlson, “The Origin(s) of the 'Caesarean' Text,” 20-21. Carlson includes P45, W, Families 1 and 13, 28, Codex Bobbiensis (i.e. Old Latin k), and Origen's text in his “Branch gamma.”
[32] Amy S. Anderson (“Codex 1582 and Family 1 of the Gospels,” ii) acknowledges the possibility of a connection between Family 1 and Caesarea although in the Gospel of Matthew rather than Mark: “The text and marginal variants of Codex 1582 are shown to be related, though not identical to the text of Matthew used by Origen, raising the possibility of a Caesarean archetype.” Anderson proposes that 1582 should be considered the leading member of Family 1 in Matthew.
[33] Wisse, Profile Method, chapters 5 and 6. Wisse's groups relate to the Gospel of Luke but often carry over to Mark. The table only includes those groups by von Soden and Wisse which correlate well with the PAM groups.
[34] Strutwolf and Wachtel, Parallel Pericopes, 5*, suggest that the Saba manuscripts (Gregory-Aland numbers 1328-1348) “may help to answer whether common location results in textual similarity.”
[35] The distance matrices used to obtain these results were calculated by the R script named dist.r. Rather than select only those variation units where the reference witness (i.e. the one to be retained) is defined, the program detects the two least well defined witnesses on every iteration. It normally drops the least well defined but will drop the second one if the first is the reference witness. If the witness to be retained is not defined for the minimum number of variation units then the procedure is abandoned at the outset. The proportion of variance figures for the UBS4 and INTF CMDS maps for P45 are 0.56 and 0.32, respectively.
[36] In the preface to the fifth impression of his Four Gospels, Streeter quotes Kenyon's assessment that the character of the text of P45 in Mark is “definitely Caesarean.”
[37] The dist.r script produced the distance matrix for Origen using the same algorithm as mentioned before. The proportion of variance figure for the CMDS map is 0.54, indicating that it conveys just over half of the information in the distance matrix. No results are presented for the INTF data set because it does not include patristic citations.
[38] Streeter, Four Gospels, 101-2.
[39] The original data matrix was divided into submatrices using the R script named from-1-to-N.r. This script produces submatrices with the same set of cases (i.e. witnesses) but a subset of variables (i.e. variation units). The submatrices have approximately equal numbers of variables. The proportion of variance figures for the CMDS maps are 0.45, 0.53, 0.50, and 0.47, respectively.
[40] Nevertheless, the script which constructs a distance matrix can be instructed do retain a specific case so it is often possible to obtain analysis results for omitted witnesses if desired.
[41] Sanders, Washington Manuscript of the Four Gospels, 73; Streeter, Four Gospels, 598-600. Streeter also gives an imaginative account of how 032 might have acquired the mixture of texts it preserves.
[42] The biplot was produced by the R script named MVA-MCA.r which uses the “mca” method of the “MASS” package. (See Venables and Ripley, Modern Applied Statistics with S.) The script drops witnesses which have undefined readings in any variation units prior to analysis. Concerning categorical data, the only meaningful basis for comparison is equivalence. For example, when comparing the encoded readings of two witnesses at a variation site, one can only say whether they are the same or different; it does not make sense to say that one reading is more or less than the other in this context. Even though New Testament textual data is treated as categorical in this article, the readings of a variation unit can have an inherent order. In fact, the INTF's Coherence-Based Genealogical Method relies on there being a discernible order of development for the readings of a variation unit.
[43] Wisse, Profile Method, 6.
[44] Ernest C. Colwell and Ernest W. Tune, "Establishing Quantitative Relationships," 59.
[45] Others have noted practical weaknesses in Colwell's definition of a group. W. L. Richards (Classification of the Greek Manuscripts of the Johannine Epistles) writes (43) “If one were to use 70 percent, let us say, as a minimum percentage for showing a text-type, then we would have to conclude that there is no such thing as a distinction between the Byzantine and Alexandrian text-types.” Using the example of percentage agreements with Codex Sinaiticus, Richards goes on to say (53) “As far as the 10 percent gap is concerned, there is no noticeable gap at all below the 70 percent line.” According to Klaus Wachtel ("Colwell Revisited," 39), Colwell's criteria for defining a text-type, including that group members should share exclusive group readings, are very unlikely to be met when the analysis is based on comprehensive evidence.
[46] B. F. Westcott and F. J. A. Hort, Introduction, 40.